Ask The Wizard #411
I contend that if casinos had a 0% house edge on every game they would still make money. This is because of bad money management by players and players have a limited bankroll compared to the casino. Do you agree?
No, I disagree.
Money management is overrated. It doesn't matter how player's play a game of luck like roulette, the house edge cannot be dented in either direction.
As to the argument that the casino can simply outlast the player until he goes bust, it is possible the casino will go bust first. Consider a player with a $10,000 bankroll against any MGM-Mirage casino. The market cap of MGM-Mirage, at the time of this writing, is $11,168,000,000. Further assume, for the sake of argument, the company owned 100% of its stock. If the player played until either side went bust, he would have a 1 in 1,116,801 chance of winning the entire company. Given the large player volume, eventually some player would be successful.
I know that each state gets a number of Congressional seats according to it's population. However, how do they do it exactly? There must be some method of doing the math. Is it possible that a state could increase in population, with the total population remaining the same, and lose a seat?
The short answer is each state starts with at least one. Then, each additional seat is awarded one at a time to the state that would realize the "greatest benefit" from that seat.
It gets more complicated in how the "greatest benefit" is calculated. Here are the details:
- Calculate the "multiplier" as the geometric mean of (1) the percentage increase in total seats with the extra seat and (2) the percentage increase in total seats if the state had one more seat than it actually does. To put it in a formula, if n is the current number of seats, then the multiplier is 1/sqrt(n*(n+1)).
- Calculate the "priority value" as the product of the multiplier and population of the state.
Do this calculation for every state. The state with the greatest priority value gets the next seat.
Let's look at Nevada, for example. The 2020 population was 3,104,614 and it already has 4 seats. The multiplier is 1/sqrt(4*5) = 1/sqrt(20) = 0.223607. The priority value is 3,104,614 * 0.223607 = 694,213.
Not that you asked, but if the congress added a 436th seat, it would go to New York. The following table shows priority value for all 50 states in order.
| State | Population | Current Seats | Multiplier | Priority Value |
|---|---|---|---|---|
| New York | 20,201,249 | 26 | 0.037743 | 762,447 |
| Ohio | 11,799,448 | 15 | 0.064550 | 761,651 |
| Texas | 29,145,505 | 38 | 0.025976 | 757,090 |
| Florida | 21,538,187 | 28 | 0.035093 | 755,842 |
| Arizona | 7,151,502 | 9 | 0.105409 | 753,835 |
| California | 39,538,223 | 52 | 0.019048 | 753,143 |
| Virginia | 8,631,393 | 11 | 0.087039 | 751,266 |
| Idaho | 1,839,106 | 2 | 0.408248 | 750,812 |
| Michigan | 10,077,331 | 13 | 0.074125 | 746,981 |
| New Jersey | 9,288,994 | 12 | 0.080064 | 743,715 |
| Pennsylvania | 13,002,700 | 17 | 0.057166 | 743,315 |
| Massachusetts | 7,029,917 | 9 | 0.105409 | 741,018 |
| Georgia | 10,711,908 | 14 | 0.069007 | 739,192 |
| Washington | 7,705,281 | 10 | 0.095346 | 734,670 |
| Illinois | 12,812,508 | 17 | 0.057166 | 732,442 |
| West Virginia | 1,793,716 | 2 | 0.408248 | 732,281 |
| Utah | 3,271,616 | 4 | 0.223607 | 731,556 |
| Tennessee | 6,910,840 | 9 | 0.105409 | 728,466 |
| Maryland | 6,177,224 | 8 | 0.117851 | 727,993 |
| Missouri | 6,154,913 | 8 | 0.117851 | 725,363 |
| Oklahoma | 3,959,353 | 5 | 0.182574 | 722,876 |
| North Carolina | 10,439,388 | 14 | 0.069007 | 720,386 |
| Louisiana | 4,657,757 | 6 | 0.154303 | 718,708 |
| Indiana | 6,785,528 | 9 | 0.105409 | 715,257 |
| Iowa | 3,190,369 | 4 | 0.223607 | 713,388 |
| Delaware | 989,948 | 1 | 0.707107 | 699,999 |
| Kentucky | 4,505,836 | 6 | 0.154303 | 695,266 |
| Wisconsin | 5,893,718 | 8 | 0.117851 | 694,581 |
| Nevada | 3,104,614 | 4 | 0.223607 | 694,213 |
| South Carolina | 5,118,425 | 7 | 0.133631 | 683,978 |
| Colorado | 5,773,714 | 8 | 0.117851 | 680,439 |
| Arkansas | 3,011,524 | 4 | 0.223607 | 673,397 |
| Minnesota | 5,706,494 | 8 | 0.117851 | 672,517 |
| Alabama | 5,024,279 | 7 | 0.133631 | 671,398 |
| Mississippi | 2,961,279 | 4 | 0.223607 | 662,162 |
| Connecticut | 3,605,944 | 5 | 0.182574 | 658,352 |
| Kansas | 2,937,880 | 4 | 0.223607 | 656,930 |
| Oregon | 4,237,256 | 6 | 0.154303 | 653,823 |
| South Dakota | 886,667 | 1 | 0.707107 | 626,968 |
| New Mexico | 2,117,522 | 3 | 0.288675 | 611,276 |
| Hawaii | 1,455,271 | 2 | 0.408248 | 594,112 |
| Nebraska | 1,961,504 | 3 | 0.288675 | 566,237 |
| New Hampshire | 1,377,529 | 2 | 0.408248 | 562,374 |
| Maine | 1,362,359 | 2 | 0.408248 | 556,181 |
| North Dakota | 779,094 | 1 | 0.707107 | 550,903 |
| Alaska | 733,391 | 1 | 0.707107 | 518,586 |
| Vermont | 643,077 | 1 | 0.707107 | 454,724 |
| Rhode Island | 1,097,379 | 2 | 0.408248 | 448,003 |
| Montana | 1,084,225 | 2 | 0.408248 | 442,633 |
| Wyoming | 576,851 | 1 | 0.707107 | 407,895 |
| Total | 330,759,736 | 435 | 0.002296 | 759,495 |
As to your second question, yes, that is possible. I had to fidget for a while to find a situation where this happened. First consider a hypothetical country with the following six states. With 15 total seats, the allocation would be as follows:
| State | Population | Current Seats | Multiplier | Priority Value |
|---|---|---|---|---|
| Confusion | 900 | 3 | 0.288675 | 259.807621 |
| Denial | 800 | 3 | 0.288675 | 230.940108 |
| Bliss | 700 | 3 | 0.288675 | 202.072594 |
| Depression | 600 | 2 | 0.408248 | 244.948974 |
| Limbo | 500 | 2 | 0.408248 | 204.124145 |
| Anxiety | 400 | 2 | 0.408248 | 163.299316 |
| Total | 3,900 | 15 |
Next assume there was a census and the populations changed significantly, but the total remained the same at 3,900 and Anxiety increased in population from 400 to 401. It would get only one seat with 15 states.
| State | Population | Current Seats | Multiplier | Priority Value |
|---|---|---|---|---|
| Confusion | 1,885 | 7 | 0.133631 | 251.893721 |
| Denial | 405 | 2 | 0.408248 | 165.340558 |
| Bliss | 404 | 2 | 0.408248 | 164.932309 |
| Depression | 403 | 2 | 0.408248 | 164.524061 |
| Limbo | 402 | 1 | 0.707107 | 284.256926 |
| Anxiety | 401 | 1 | 0.707107 | 283.549819 |
| Total | 3,900 | 15 |
I wish to emphasize I had to tinker with the numbers for quite a while to find a situation where this happened. Overall, I find the method quite fair.
Two circles are inscribed in a rectangle of height 81. There is a line segment of length 56 extending to the edge of both circles and goes through where the circles meet and is parallel to the vertical edge of the rectangle.
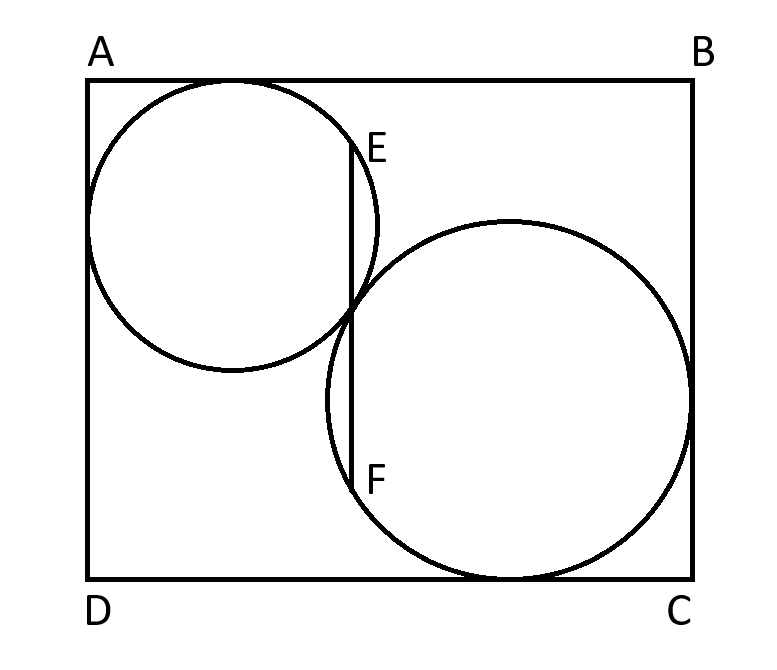
How wide is the rectangle?




