On this page
Ultimate Texas Hold 'Em - Rules and Strategy Chart
Introduction
Ultimate Texas Hold'em® is a poker-based casino game in which the player may make one raise at any time during the course of the hand. The earlier the raise is made the higher it may be. Unlike other poker-based games, raises made after the ante still have action, even if the dealer doesn't open. This game was invented by Roger Snow of Shuffle Master. The same base game is also distributed by Galaxy Gaming under the name Heads Up Hold 'Em.
ULTIMATE TEXAS HOLD ’EM® is a registered trademark of Bally Gaming, Inc. and is used with permission on this website.
 Top Ultimate Texas Hold 'Em - Rules and Strategy Chart Online Casinos
Top Ultimate Texas Hold 'Em - Rules and Strategy Chart Online Casinos
$1000 BONUS + $25FREE
Casino, Sports and Poker
Licensed in New Jersey
Deposit/Withdraw - PayPal/Visa
Collusion
Knowledge of other player cards can reduce the house edge, if the information is used properly. For an in-depth analysis of this topic, please see my page on Ultimate Texas Hold 'Em Collusion.
How To Video
Rules
Following are the standard rules as played in the United States. There is a variant played in Auckland, New Zealand, I address following the standard rules.
- The game is played with a single ordinary 52-card deck.
- The player must make an equal bet on both the Ante and Blind, and can also make an optional Trips bet.
- Two cards are dealt face down to the player and dealer. The player may look at his own cards.
- The player can check or make a Play bet equal to three or four times the Ante.
- The dealer turns over three community cards.
- If the player previously checked, then he may make a Play bet equal to two times his Ante. If the player already made a Play bet, then he may not bet further.
- Two final community cards are turned over.
- If the player previously checked twice, then he must either make a Play bet equal to exactly his Ante, or fold, losing both his Ante and Blind bets. If the player already raised he may not bet further.
- The player and dealer will both make the best possible hand using any combination of their own two cards and the five community cards.*
- The dealer will need at least a pair to open.
- The following table shows how the Blind, Ante, and Play bets are scored, according to who wins, and whether the dealer opens.
Scoring Rules
Winner Dealer Opens Blind Ante Play Player Yes Win Win Win Player No Win Push Win Dealer Yes Lose Lose Lose Dealer No Lose Push Lose Tie Yes or No Push Push Push - Winning Ante and Play bets pay 1 to 1. Winning Blind bets pay according to the following pay table.
Blind Bet Pay Table
Player Hand Pays Royal flush 500 to 1 Straight flush 50 to 1 Four of a kind 10 to 1 Full house 3 to 1 Flush 3 to 2 Straight 1 to 1 All other Push - The Trips bet will pay according to the poker value of the player's hand regardless of the value of the dealer's hand, according to one of the Trips bet pay tables below.
Notes:
* While the standard rules let both player and dealer use any five cards to make their best poker hand, in Auckland, New Zeland, both sides must make use of both hole cards and three of the five community cards. An analysis of the game under this rule can be found in my page on Ultimate Texas Hold 'Em -- Auckland Variant.
Analysis
There are 52 possible outcomes of each hand. The table below shows the probability of each and the contribution to the total return, assuming optimal strategy. A 4X raise is referred to as a "large raise," a 2X raise as "medium," and 1x as "small."
The lower right cell shows a house edge of 2.185% per ante bet. What this means, for example, is if you bet $1 and both the Ante and Blind initially, then you can expect to lose 2.185 cents on average. However for comparison to other games I believe the Element of Risk is more appropriate to look at. The average total amount bet by the end of the hand is 4.152252 times the ante bet. So the element of risk would be 2.185%/4.152252 = 0.526%. The standard deviation, relative to the Ante bet, is 4.94.
Large bettors should be wary of maximum payouts. If your ante bet is more than 1/500 of the maximum payout, then you will get shortchanged on a royal flush. For every 100 the effective payout on a royal goes down, the house edge will go up by 0.308%. In other words, the increase in the house edge will be [500-(MP/500)]*0.0000308, where MP is the maximum payout.
The next table shows the average wager and return from each bet.
Ultimate Texas Hold 'Em® Return Table
| Bet Type | Average Wager |
Average Pays |
Average Win |
|---|---|---|---|
| Ante | 1 | -0.165757 | -0.165757 |
| Blind | 1 | -0.314685 | -0.314685 |
| Play | 2.152252 | 0.213076 | 0.458593 |
| Total | 4.152252 | -0.02185 |
Wizard Strategy
The following is my "Wizard Strategy" for Ultimate Texas Hold 'Em®.
Large Raise: The following table shows when to make the 4X raise.
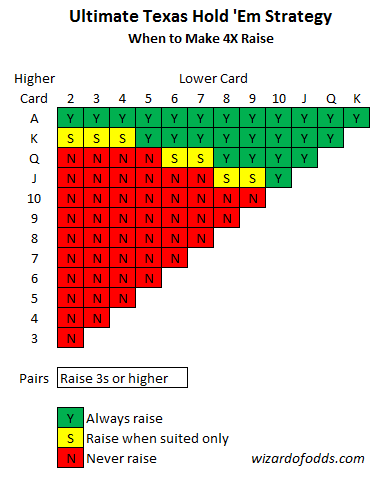
Medium Raise: Make the 2X raise with any of the following:
- Two pair or better.
- Hidden pair*, except pocket deuces.
- Four to a flush including a hidden 10 or better to that flush
* Hidden pair = Any pair with at least one card in your hole cards (thus the pair is hidden to the dealer).
Small Raise: Make the 1X raise with any of the following, otherwise fold:
- Hidden pair or better.
- Less than 21 dealer outs beat you.
Example
What I mean by an "out" is a dealer hole card that will cause you to lose. Let's look at this situation as an example.

In the example above, there 15 cards that will pair the dealer and beat you (three suits each of K, 7, 2, A, and 10). Then there are the two ranks (jacks and queens) which will out-kick the player. All four jacks and queens remain in the decks, so that is 2×4=8 more cards that will beat you. So, we're up to 15+8=23. We don't count the other three nines because those will result in a push. So, because there are only 23 outs (21 or more), we fold.
BTW, using my Ultimate Texas Hold 'Em® calculator, we see that the expected value of raising this hand is -2.136364, which is less than the -2 of folding.
I get asked a lot about combinations of cards that will beat the player. For example, any two dealer spades that would give the dealer a flush in the example above. The answer is no. It would really make things complicated if the strategy accounted for double-card combinations that would beat the player.
Following my Wizard strategy will result in a house edge of 2.43% and an Element of Risk of 0.58%.
The second and third decision points are influenced by the James Grosjean strategy, for which I have great respect, as I do for all of Grosjean's work. I highly recommend his strategy if you want to something even more powerful than my simple strategy above.
Trips Bet
Shufflemaster literature mentions the following four possible pay tables on the Trips bet.
Trips Bet - Pay Table 1
| Player Hand | Combinations | Pays | Probability | Return |
|---|---|---|---|---|
| Royal flush | 4324 | 50 | 0.000032 | 0.001616 |
| Straight flush | 37260 | 40 | 0.000279 | 0.01114 |
| Four of a kind | 224848 | 30 | 0.001681 | 0.05042 |
| Full house | 3473184 | 9 | 0.025961 | 0.233649 |
| Flush | 4047644 | 7 | 0.030255 | 0.211785 |
| Straight | 6180020 | 4 | 0.046194 | 0.184775 |
| Three of a kind | 6461620 | 3 | 0.048299 | 0.144896 |
| All other | 113355660 | -1 | 0.8473 | -0.8473 |
| Total | 133784560 | 1 | -0.009018 |
Trips Bet - Pay Table 2
| Player Hand | Combinations | Pays | Probability | Return |
|---|---|---|---|---|
| Royal flush | 4324 | 50 | 0.000032 | 0.001616 |
| Straight flush | 37260 | 40 | 0.000279 | 0.01114 |
| Four of a kind | 224848 | 30 | 0.001681 | 0.05042 |
| Full house | 3473184 | 8 | 0.025961 | 0.207688 |
| Flush | 4047644 | 6 | 0.030255 | 0.18153 |
| Straight | 6180020 | 5 | 0.046194 | 0.230969 |
| Three of a kind | 6461620 | 3 | 0.048299 | 0.144896 |
| All other | 113355660 | -1 | 0.8473 | -0.8473 |
| Total | 133784560 | 1 | -0.01904 |
Trips Bet — Pay Table 3
| Player Hand | Combinations | Pays | Probability | Return |
|---|---|---|---|---|
| Royal flush | 4324 | 50 | 0.000032 | 0.001616 |
| Straight flush | 37260 | 40 | 0.000279 | 0.01114 |
| Four of a kind | 224848 | 30 | 0.001681 | 0.05042 |
| Full house | 3473184 | 8 | 0.025961 | 0.207688 |
| Flush | 4047644 | 7 | 0.030255 | 0.211785 |
| Straight | 6180020 | 4 | 0.046194 | 0.184775 |
| Three of a kind | 6461620 | 3 | 0.048299 | 0.144896 |
| All other | 113355660 | -1 | 0.8473 | -0.8473 |
| Total | 133784560 | 1 | -0.034979 |
Pay table #3 seen at the Mirage.
Trips Bet - Pay Table 4
| Player Hand | Combinations | Pays | Probability | Return |
|---|---|---|---|---|
| Royal flush | 4324 | 50 | 0.000032 | 0.001616 |
| Straight flush | 37260 | 40 | 0.000279 | 0.01114 |
| Four of a kind | 224848 | 20 | 0.001681 | 0.033613 |
| Full house | 3473184 | 7 | 0.025961 | 0.181727 |
| Flush | 4047644 | 6 | 0.030255 | 0.18153 |
| Straight | 6180020 | 5 | 0.046194 | 0.230969 |
| Three of a kind | 6461620 | 3 | 0.048299 | 0.144896 |
| All other | 113355660 | -1 | 0.8473 | -0.8473 |
| Total | 133784560 | 1 | -0.061808 |
Pay table #4 seen at Shufflemaster TableMax units.
Common Progressive
This is the most common progressive jackpot, in my experience, so I'll title it the "Common Progressive." I used to title it the "Michigan Progressive," when the only known placement was in Michigan, but now it is seen all over the place.
There is just a single bet amount, which can be $1 or $5, depending on the table. Wins are based on the player's two hole cards and the three flop cards. The following table shows the probability and contribution to the return for the various wins. Wins are relative to the amount bet and are on a "for one" basis.
Common Progressive
| Event | Pays | Envy Bonus |
Combinations | Probability | Return | Envy Return |
|---|---|---|---|---|---|---|
| Royal flush | 100% of jackpot | 1000 | 4 | 0.000002 | 0.000000 | 0.001539 |
| Straight flush | 10% of jackpot | 300 | 36 | 0.000014 | 0.000000 | 0.004156 |
| Four of a kind | 300 | 624 | 0.000240 | 0.072029 | 0.000000 | |
| Full house | 50 | 3,744 | 0.001441 | 0.072029 | 0.000000 | |
| Flush | 40 | 5,108 | 0.001965 | 0.078616 | 0.000000 | |
| Straight | 30 | 10,200 | 0.003925 | 0.117739 | 0.000000 | |
| Three of a kind | 9 | 54,912 | 0.021128 | 0.190156 | 0.000000 | |
| Total | 74,628 | 0.028715 | 0.530569 | 0.005695 |
What the table above immediately shows us is fixed wins return 53.06% to the player. For each additional player at the table, besides yourself, your return goes up by 0.57% from the Envy Bonus.
For a $1 bet, every $10,000 in the meter adds 2.924% to the return. Likewise, for a $5 bet, every $50,000 in the meter adds 2.924% to the return.
The next table shows the break-even point, where the Progressive side bet has zero house edge, according to the bet amount and number of other players (not counting yourself).
Common Progressive
| Other Players |
$1 Bet | $5 Bet |
|---|---|---|
| 0 | $160,530.53 | $802,652.63 |
| 1 | $158,583.16 | $792,915.79 |
| 2 | $156,635.79 | $783,178.95 |
| 3 | $154,688.42 | $773,442.11 |
| 4 | $152,741.05 | $763,705.26 |
| 5 | $150,793.68 | $753,968.42 |
Small Progressive
Many tables in Las Vegas offer a $1 progressive side bet. The top win is for a royal flush using at least one hole card, which I call a "hidden royal flush." There is also a $100 envy bonus if another player gets a hidden royal. The following table shows the return of the fixed wins only, not counting the envy bonus. It shows a return of 45.68%, before considering the jackpot and envy bonuses.
Small Progressive
| Event | Pays | Envy | Combinations | Probability | Return |
|---|---|---|---|---|---|
| Hidden royal flush | Jackpot | $100 | 86,480 | 0.000031 | ? |
| Community royal flush | $1000 | $0 | 4,324 | 0.000002 | 0.001539 |
| Straight flush | $250 | $0 | 782,460 | 0.000279 | 0.069627 |
| Four of a kind | $75 | $0 | 4,721,808 | 0.001681 | 0.126050 |
| Full house | $10 | $0 | 72,936,864 | 0.025961 | 0.259610 |
| All other | $0 | $0 | 2,730,943,824 | 0.972047 | 0.000000 |
| Total | 2,809,475,760 | 1.000000 | 0.456827 + ? |
The return per $1000 in jackpot is 3.08%. The return for the Envy Bonus is 0.308% for each additional player at the table. So each additional player at the table is worth $100 in the meter.
The next table shows how big the jackpot has to be for the Small Progressive to have exactly a 100% return, or zero house advantage.
Break Even Jackpots
| Other Players |
Jackpot |
|---|---|
| 5 | $17,146.07 |
| 4 | $17,246.07 |
| 3 | $17,346.07 |
| 2 | $17,446.07 |
| 1 | $17,546.07 |
| 0 | $17,646.07 |
Buffalo Thunder Progressive
The Big Progressive tends to be much larger, because the player must flop a royal flush to win it. In other words, the player cannot make use of the Turn and River cards to win the progressive, unlike in the Small Progressive. There is no Envy Bonus. It was seen at the Buffalo Thunder casino in New Mexico.
Buffalo Thunder Progressive
| Event | Pays | Permutations | Probability | Return |
|---|---|---|---|---|
| Player flops royal | 100% of jackpot | 1037760 | 0.000002 | ? |
| Royal partially on board | 5% of jackpot | 19717440 | 0.000029 | ? |
| Royal entirely on board | 3000 | 1037760 | 0.000002 | 0.004617 |
| Straight flush | 250 | 187790400 | 0.000279 | 0.069627 |
| Four of a kind | 100 | 1133233920 | 0.001681 | 0.168067 |
| Full house | 10 | 17504847360 | 0.025961 | 0.25961 |
| All other | 0 | 655426517760 | 0.972047 | 0 |
| Total | 674274182400 | 1 | 0.502077 + ? |
The return for at any given time is 50.19% plus 3.00% for each $10,000 in the meter. For exactly zero house edge, the meter would need to be $165,959.74. I'm told the meter is seeded at $5,000, and 27% of money bet goes towards the meter. Fixed wins are not deducted from the meter. That would make the overall return 77.96%.
Bad Beat Bonus
At the Admiral casino in Liechtenstein there is a Bad Beat Bonus side bet. It pays if either the player or dealer lose with a three of a kind or better. Gaming literature mentions two different pay tables. My analysis of both is below. The bottom line is a house edge of 14.79% on pay table 1 and 20.39% on pay table 2.
Bad Beat Bonus — Pay Table 1
| Losing Hand | Pays | Combinations | Probability | Return |
|---|---|---|---|---|
| Straight flush | 7,500 | 10,300,592 | 0.000004 | 0.027776 |
| Four of a kind | 500 | 471,040,512 | 0.000169 | 0.084677 |
| Full house | 50 | 8,435,225,376 | 0.003033 | 0.151637 |
| Flush | 30 | 19,434,208,592 | 0.006987 | 0.209618 |
| Straight | 20 | 18,271,076,976 | 0.006569 | 0.131381 |
| Three of a kind | 9 | 64,049,759,448 | 0.023028 | 0.207252 |
| Low hand win* | -1 | 2,557,579,127,088 | 0.919536 | -0.919536 |
| Tie | -1 | 113,130,263,816 | 0.040674 | -0.040674 |
| Total | 2,781,381,002,400 | 1.000000 | -0.147868 |
Bad Beat Bonus — Pay Table 2
| Losing Hand | Pays | Combinations | Probability | Return |
|---|---|---|---|---|
| Straight flush | 10,000 | 10,300,592 | 0.000004 | 0.037034 |
| Four of a kind | 500 | 471,040,512 | 0.000169 | 0.084677 |
| Full house | 40 | 8,435,225,376 | 0.003033 | 0.121310 |
| Flush | 25 | 19,434,208,592 | 0.006987 | 0.174681 |
| Straight | 20 | 18,271,076,976 | 0.006569 | 0.131381 |
| Three of a kind | 9 | 64,049,759,448 | 0.023028 | 0.207252 |
| Low hand win* | -1 | 2,557,579,127,088 | 0.919536 | -0.919536 |
| Tie | -1 | 113,130,263,816 | 0.040674 | -0.040674 |
| Total | 2,781,381,002,400 | 1.000000 | -0.203873 |
*: A "low hand win" is a winning hand of two pair or less.
Hole Card Bonus
I'm told this side bet can be found in Washington state, the Flamingo in Las Vegas, and Norwegian cruise ship casinos. It pays based on the player's hole cards, except the top award also involves the dealer's hole cards. The lower right cell in the following table shows a house edge of 8.54%.
Hole Card Bonus
| Bet | Pays | Combinations | Probability | Return |
|---|---|---|---|---|
| Player and dealer have aces | 1000 | 6 | 0.000004 | 0.003694 |
| Pair of aces | 30 | 7,344 | 0.004521 | 0.135636 |
| A/K suited | 25 | 4,900 | 0.003017 | 0.075415 |
| A/Q or A/J suited | 20 | 9,800 | 0.006033 | 0.120664 |
| AK off-suit | 15 | 14,700 | 0.009050 | 0.135747 |
| Pair J's - K's | 10 | 22,050 | 0.013575 | 0.135747 |
| A/Q or A/J off-suit | 5 | 29,400 | 0.018100 | 0.090498 |
| Pair 2's - 10's | 3 | 66,150 | 0.040724 | 0.122172 |
| All other | -1 | 1,470,000 | 0.904977 | -0.904977 |
| Total | 1,624,350 | 1.000000 | -0.085406 |
Australian Rules
I have an unconfirmed report that at the Crown casino in Perth, Australia, the blind bet pushes if the dealer doesn't qualify and the dealer wins. Assuming no change in strategy, this happens 1 in every 176 hands. When it happens, the player will lose one less unit. The effect is a reduction in the house edge from 2.185% to 1.617%.
.6-Card Bonus
Some casinos add on a side bet known as the 6-Card Bonus. This side bet is found on multiple poker-derivative games, so I created a special page for it. For more information, please see my page on the 6-Card Bonus.
Millionaire Progressive
This is a $5 "red light" progressive side bet that pays $1,000,000 for a royal flush in spades, I believe using the player's two hole cards and the flop. For all the rules and analysis, please see my page on the Millionaire Progressive.
Play for Free
I'm very proud to offer my Ultimate Texas Hold 'Em® game. What I'm especially pleased with is the advice feature, which offers advice based on optimal strategy. Webmaster J.B. worked very hard on this so please have a look.
Calculator
I'm proud to present my Ultimate Texas Hold 'Em® calculator. Put in any cards after the flop, river, or turn, and it will tell you the correct play and expected value.
Ask Michael Anything - Ultimate Texas Hold'em Edition
Internal Links
- Ultimate Texas Hold 'Em® game. Play for free with an advice feature to catch your mistakes.
- Ultimate Texas Hold 'Em® calculator. Put in any cards to determine the best play.
- Ultimate Texas Hold 'Em® appendix 1. Details on the odds before the flop.
- Heads Up Hold 'Em. Similar game, offering bad beat bonuses, but 3x raise only after two cards.
External Links
- Wikipedia — Entry on Ultimate Texas Hold 'Em.
- Discountgambling.net has an outstanding analysis of this game, including what I call his "nut kicker" strategy for the second and third decision points.
- Shufflemaster's Ultimate Texas Hold 'Em® page.
- Demo game — Play this licensed demo game at our sister site Latest Casino Bonuses.




