On this page
Bonus Craps
Introduction
Bonus Craps is a set of three side bets found in craps. There are as follows:
- Small — Wins if the shooter rolls every total from 2 to 6, before rolling a total of 7. Wins usually pay 30 to 1.
- Tall — Wins if the shooter rolls every total from 8 to 12, before rolling a total of 7. Wins usually pay 30 to 1.
- All — Wins if the shooter rolls every total from 2 to 12, except a 7, before rolling a total of 7. Wins usually pay 150 to 1.
In 2021, I started to see these same bets called "Diceology" at the Venetian.
Analysis
The following table shows my analysis of the Small and Tall bets, when wins pay 30 to 1. The lower right cell shows a house edge of 18.30%.
Small and Tall
| Event | Pays | Probability | Return |
|---|---|---|---|
| Win | 30 | 0.026354 | 0.790617 |
| Loss | -1 | 0.973646 | -0.973646 |
| Total | 1.000000 | -0.183029 |
In the past, some tables were known to pay 34 to 1 on the Small and Tall. These more generous odds have a house edge of 7.76%.
The following table shows my analysis of the All bet, when wins pay 150 to 1. The lower right cell shows a house edge of 20.61%.
All
| Event | Pays | Probability | Return |
|---|---|---|---|
| Win | 150 | 0.005258 | 0.788655 |
| Loss | -1 | 0.994742 | -0.994742 |
| Total | 1.000000 | -0.206087 |
I have seen other pays on the All bet, including 155 and 175 to 1. Remember to subtract one from a pay to convert from "for one" to "to one" odds. The following table shows the house edge for all pays evenly divisible by 5 from 150 to 175.
House Edge Summary on All Bet
| Pays | House Edge |
|---|---|
| 150 | 20.61% |
| 155 | 17.98% |
| 160 | 15.35% |
| 165 | 12.72% |
| 170 | 10.09% |
| 175 | 7.46% |
Methodology
I've analyzed Bonus Craps three ways, as follows:
- Simulation — This is probably the easiest way. However, for mathematical purists like me, simulations are always so intellectually unsatisfying.
- Markov Chain — This method is tedious and time consuming. For the Small and Tall it would require a 6x6 transition matrix and for the All a 12x12.
- Integral Calculus — This method is surprisginly easy with the use of an integral calculator. I explain it in more depth below.
Imagine that instead of significant events being determined by the roll of dice, one at a time, consider them as an instant in time. Assume the time between events has a memory-less property, with an average time between events of one unit of time. In other words, the time between events follows an exponetial distribution with a mean of 1. This will not matter for purposes of adjudicating the bet, because events still happen one at a time.
The following is the probability any given total has NOT been rolled at least once within x units of time:
- 2 or 12: exp(-x/36)
- 3 or 11: exp(-x/18)
- 4 or 10: exp(-x/12)
- 5 or 9: exp(-x/9)
- 6 or 8: exp(-5x/36)
- 7: exp(-x/6)
Let's look at the Small bet first. The odds are exactly the same for the Tall bet.
In x units of time, the probability that the 2, 3, 4, 5, and 6 have been rolled, and the 7 has not is: (1-exp(-x/36))*(1-exp(-x/18))*(1-exp(-x/12))*(1-exp(-x/9))*(1-exp(-5x/36))*exp(-x/6) The probability that at time x, the player rolls a 7, having previously rolled every total from 2 to 6, is:
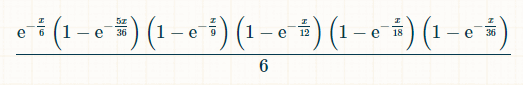
For the integration,I used this integral calculator.
Since a winning 7 could happen at any time, the probability of winning is the integral of this probability over x from 0 to infinity. Not that we need to know, but the integral is, before putting in the limits of integration is (-6*e^(-x/6)+(36*e^(-(7*x)/36))/7+(9*e^(-(2*x)/9))/2-(36*e^(-(11*x)/36))/11-3*e^(-x/3)-(36*e^(-(13*x)/36))/13+(18*e^(-(7*x)/18))/7+(12*e^(-(5*x)/12))/5+(9*e^(-(4*x)/9))/4-(36*e^(-(19*x)/36))/19-(9*e^(-(5*x)/9))/5+(12*e^(-(7*x)/12))/7)/6.
Putting in the limits of integration, the answer is 20049 / 760760 = apx. 0.02635390924864609.
Next, let's look at the All bet.
In x units of time, the probability that the 2, 3, 4, 5, 6, 8, 9, 10, 11, and 12 have been rolled, and the 7 has not is: (1-exp(-x/36))2*(1-exp(-x/16))2*(1-exp(-x/12))2*(1-exp(-x/9))2*(1-exp(-5x/36))2*exp(-x/6) The probability that at time x, the player rolls a 7, having previously rolled every total from 2 to 6, is:

Since a winning 7 could happen at any time, the probability of winning is the integral of this probability over x from 0 to infinity. Not that we need to know, but the integral is, before putting in the limits of integration is (-6*e^(-x/6)+(72*e^(-(7*x)/36))/7+(9*e^(-(2*x)/9))/2-8*e^(-x/4)-(18*e^(-(5*x)/18))/5-(72*e^(-(11*x)/36))/11+(72*e^(-(13*x)/36))/13+(108*e^(-(7*x)/18))/7+(24*e^(-(5*x)/12))/5-(27*e^(-(4*x)/9))/4-(216*e^(-(17*x)/36))/17-10*e^(-x/2)-(72*e^(-(19*x)/36))/19+(27*e^(-(5*x)/9))/5+(144*e^(-(7*x)/12))/7+(54*e^(-(11*x)/18))/11-(72*e^(-(23*x)/36))/23-(15*e^(-(2*x)/3))/2-(216*e^(-(25*x)/36))/25-(54*e^(-(13*x)/18))/13+(8*e^(-(3*x)/4))/3+(54*e^(-(7*x)/9))/7+(72*e^(-(29*x)/36))/29-(72*e^(-(31*x)/36))/31-(9*e^(-(8*x)/9))/8-(24*e^(-(11*x)/12))/11+(18*e^(-(17*x)/18))/17+(72*e^(-(35*x)/36))/35-e^(-x))/6.
Putting in the limits of integration, the answer is 126538525259 / 24067258815600 = 0.0052577040961964420049.





