On this page
Opponent Poker
Introduction
Opponent Poker is a video poker variation I noticed at the Red Rock Resort on December 17, 2006. The first five credits bet plays like ordinary video poker, and the second five credits are pooled together with two computer opponents, the best video poker hand takes all.
Rules
- The player may bet 0, 1, 2, 3, 4, 5, or 10 credits.
- If the player bets 5 or fewer credits the game will play like ordinary video poker.
- If the player bets ten credits, five will act as a normal video poker bet. The other five credits will be used to play against two computer opponents.
- Assuming ten credits are bet, after the initial five cards are dealt both computer opponents will indicate which cards they will hold. According to the game rules the opponent strategy is "a standard poker strategy." I do not know this strategy, but based on playing Opponent Poker myself it is usually, but not always, optimal video poker strategy.
- The player will choose which cards he wishes to hold.
- The player and both opponents will be dealt replacement cards from the same 52-card deck.
- If the player has a higher paying video poker hand than the other two computer opponents then he shall win the video poker winnings from all three hands.
- In the event two or three participants tie for the highest paying video poker hand then the pot of combined video poker winnings shall carry over to the next hand.
- In the event of a tie between hands the player may opt to split the pot. Split pots will be rounded down to the nearest credit.
- The pot will automatically be split if there is a dealt royal flush, the player cashes out, or the player switches games.
Strategy
I don't know what the "standard poker strategy" for the computer opponents is so I can not quantify an optimal player strategy. I tend to think that if the player followed optimal video poker strategy for the given pay table his return would be greater than that of conventional video poker. The player should not always play the same way as the computer opponents. As one example the hand on the deal wasK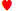 A
A Q
Q 8
8 9
9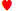 .Both computer opponents held the queen, king, and ace. Optimal video poker strategy is to hold the king and queen only. Holding the same cards as the computer opponents always results in the same expected value as conventional video poker. In this case holding the three high cards has an expected value of 4.560592 credits (2.280296 credits for both the video poker and opponent bet). Holding the queen and king only has an expected value of 4.863301 credits (2.397471 for the video poker hand and 2.46583 for the opponent bet). This just goes to show (1) the opponents don't always follow optimal video poker strategy, and (2) you should not always play the same way as the opponents.
.Both computer opponents held the queen, king, and ace. Optimal video poker strategy is to hold the king and queen only. Holding the same cards as the computer opponents always results in the same expected value as conventional video poker. In this case holding the three high cards has an expected value of 4.560592 credits (2.280296 credits for both the video poker and opponent bet). Holding the queen and king only has an expected value of 4.863301 credits (2.397471 for the video poker hand and 2.46583 for the opponent bet). This just goes to show (1) the opponents don't always follow optimal video poker strategy, and (2) you should not always play the same way as the opponents.
Return
As stated in the strategy section I don't know "standard poker strategy" and thus can neither quantify either a perfect strategy nor the maximum return. All I can do is indicate the return tables for the video poker tables observed at the Red Rock Resort. I do believe the maximum return is slightly higher than the returns below.
"9/5" Jacks or Better
| Hand | Payoff | Combinations | Probability | Return |
|---|---|---|---|---|
| Royal flush | 800 | 496237776 | 0.000025 | 0.019916 |
| Straight flush | 50 | 2137447980 | 0.000107 | 0.005362 |
| 4 of a kind | 25 | 47100799404 | 0.002363 | 0.059073 |
| Full house | 9 | 229510637676 | 0.011514 | 0.103626 |
| Flush | 5 | 217120426644 | 0.010892 | 0.054462 |
| Straight | 4 | 223861063908 | 0.011231 | 0.044922 |
| 3 of a kind | 3 | 1484332642620 | 0.074465 | 0.223396 |
| Two pair | 2 | 2577431192796 | 0.129303 | 0.258606 |
| Jacks or better | 1 | 4288342040640 | 0.215135 | 0.215135 |
| Nothing | 0 | 10862898027756 | 0.544964 | 0.000000 |
| Total | 0 | 1.000000 | 0.984498 |
"8/5" Bonus Poker Deluxe
| Hand | Payoff | Combinations | Probability | Return |
|---|---|---|---|---|
| Royal flush | 800 | 491855652 | 0.000025 | 0.019740 |
| Straight flush | 50 | 2154130740 | 0.000108 | 0.005403 |
| 4 of a kind | 80 | 47005788324 | 0.002358 | 0.188653 |
| Full house | 8 | 228890564676 | 0.011483 | 0.091863 |
| Flush | 5 | 216493699248 | 0.010861 | 0.054305 |
| Straight | 4 | 260258167080 | 0.013056 | 0.052226 |
| 3 of a kind | 3 | 1475243948064 | 0.074009 | 0.222028 |
| Two pair | 1 | 2556435840408 | 0.128250 | 0.128250 |
| Jacks or better | 1 | 4216703051664 | 0.211541 | 0.211541 |
| Nothing | 0 | 10929553471344 | 0.548308 | 0.000000 |
| Total | 19933230517200 | 1.000000 | 0.974009 |
"9/5" Double Double Bonus — 97.87%
| Hand | Payoff | Combinations | Probability | Return |
|---|---|---|---|---|
| Royal flush | 800 | 497516688 | 0.000025 | 0.019967 |
| Straight flush | 50 | 2123092824 | 0.000107 | 0.005326 |
| 4 aces + 2-4 | 400 | 1228310184 | 0.000062 | 0.024648 |
| 4 2-4 + A-4 | 160 | 2854473252 | 0.000143 | 0.022912 |
| 4 aces + 5-K | 160 | 3459809880 | 0.000174 | 0.027771 |
| 4 2-4 + 5-K | 80 | 7662852888 | 0.000384 | 0.030754 |
| 4 5-K | 50 | 32536223652 | 0.001632 | 0.081613 |
| Full house | 9 | 216639836640 | 0.010868 | 0.097814 |
| Flush | 5 | 218785162368 | 0.010976 | 0.054880 |
| Straight | 4 | 257980198392 | 0.012942 | 0.051769 |
| 3 of a kind | 3 | 1501776975600 | 0.075340 | 0.226021 |
| Two pair | 1 | 2454744788496 | 0.123148 | 0.123148 |
| Jacks or better | 1 | 4227940545588 | 0.212105 | 0.212105 |
| Nothing | 0 | 11005000730748 | 0.552093 | 0.000000 |
| Total | 0 | 19933230517200 | 1.000000 | 0.978729 |
Deuces Wild — 97.58%
| Hand | Payoff | Combinations | Probability | Return |
|---|---|---|---|---|
| Natural royal flush | 800 | 452258388 | 0.000023 | 0.018151 |
| Four deuces | 200 | 3681116136 | 0.000185 | 0.036934 |
| Wild royal flush | 20 | 35519655168 | 0.001782 | 0.035639 |
| Five of a kind | 12 | 59450103984 | 0.002982 | 0.035790 |
| Straight flush | 10 | 109163645748 | 0.005476 | 0.054765 |
| Four of a kind | 4 | 1213460173776 | 0.060876 | 0.243505 |
| Full house | 4 | 520454143512 | 0.026110 | 0.104439 |
| Flush | 3 | 420473233680 | 0.021094 | 0.063282 |
| Straight | 2 | 1160573109144 | 0.058223 | 0.116446 |
| Three of a kind | 1 | 5318990094612 | 0.266840 | 0.266840 |
| Nothing | 0 | 11091012983052 | 0.556408 | 0.000000 |
| Total | 0 | 19933230517200 | 1.000000 | 0.975791 |
One interesting thing about this game is that according to the rules the pot can grow infinitely. This does not seem to run afoul of Nevada Gaming Control Board regulation 14.2.070, which states if the probability of hitting the top jackpot is less than 1 in 100 million then that probability must be prominently displayed. On any given hand the highest award is the pot plus 8000 credits, for a dealt royal, and that probability is 1 in 649,740.




