On this page
Sic Bo Appendix
Introduction

Image take from the Claridge Hotel/Casino rule book. Click on the image to see the rules on the next page.
- Low:
This bet would have nohouse edge if it were not for the triple exception. Theprobability of a triple 1, 2, or 3 is 3/216. Theprobability of any total between 3 and 10 is 1/2, or108/216. So the probability of a winning triple is108/216 - 3/216 = 105/216. The player's edge is thus(105/216)*(+1) + (111/216)*(-1) = -6/216 =~-2.78%.
- High: See Low.
- SpecificNumber:
The probability ofrolling zero of a specific number is (5/6)3 =125/216.
The probability of rolling one of a specific number is3*(1/6)1*(5/6)2 = 75/216.
The probability of rolling two of a specific number is3*(1/6)2*(5/6)1 = 15/216.
The probability of rolling three of a specific number is(1/6)3 = 1/216.
The player's edge is thus (125/216)*(-1) + (75/216)*(+1)+ (15/216)*(+2) + (1/216)*(+3) = -17/216 =~-7.780%. - Total of4:
There are 3 ways to rolla 4: (1+1+2, 1+2+1, 2+1+1). The player's edge is thus3/216*(+60) + (213/216)*(-1) = -33/216 =-15.278%.
- Total of5:
There are 6 ways to rolla 5: (1+1+3, 1+3+1, 3+1+1, 1+2+2, 2+1+2, 2+2+1). Theplayer's edge is thus 6/216*(+30) + (210/216)*(-1) =-30/216 = -13.889%.
- Total of6:
There are 10 ways to rolla 6: (1+1+4, 1+4+1, 4+1+1, 1+2+3, 1+3+2, 2+1+3, 2+3+1,3+1+2, 3+2+1, 2+2+2). The player's edge is thus10/216*(+17) + (206/216)*(-1) = -36/216 =-16.667%.
- Total of7:
There are 15 ways to rolla 7: (1+1+5, 1+5+1, 5+1+1, 1+2+4, 1+4+2, 2+1+4, 2+4+1,4+1+2, 4+2+1, 1+3+3, 3+1+3, 3+3+1, 2+2+3, 2+3+2, 3+2+2).The player's edge is thus 15/216*(+12) + (201/216)*(-1) =-21/216 = -9.722%.
- Total of8:
There are 21 ways to rolla 8: (1-6-6 * 3 ways, 1-2-5 * 6 ways, 1-3-4 * 6 ways,2-2-4 * 3 ways, 2-3-3 * 3 ways). The player's edge isthus 21/216*(+8) + (195/216)*(-1) = -27/216 =-12.500%.
- Total of9:
There are 25 ways to rolla 9: (1-2-6 * 6 ways, 1-3-5 * 6 ways, 1-4-4 * 3 ways,2-2-5 * 3 ways, 2-3-4 * 6 ways, 3-3-3 * 1 way). Theplayer's edge is thus 25/216*(+6) + (191/216)*(-1) =-41/216 = -18.982%.
- Total of10:
There are 27 ways to rolla 10: (1-3-6 * 6 ways, 1-4-5 * 6 ways, 2-2-6 * 3 ways,2-3-5 * 6 ways, 2-4-4 * 3 ways, 3-3-4 * 3 ways). Theplayer's edge is thus 27/216*(+6) + (189/216)*(-1) =-27/216 = -12.500%.
- Total of 11: Seetotal of 10
- Total of 12: Seetotal of 9
- Total of 13: Seetotal of 8
- Total of 14: Seetotal of 7
- Total of 15: Seetotal of 6
- Total of 16: Seetotal of 5
- Total of 17: Seetotal of 4
- Twonumbers:
Lets suppose the twonumbers chosen are 1 and 2. There are 30 combinationsfeaturing a 1 and a 2: 1-2-1 * 3 ways, 1-2-2 * 3 ways,1-2-3 * 6 ways, 1-2-4 * 6 ways, 1-2-5 * 6 ways, 1-2-6 * 6ways. The player's edge is thus 30/216*(+5) +(186/216)*(-1) = -36/216 = -16.667%.
- Specifictriplet:
There is only 1 way toroll a specific triplet. The player's edge is thus1/216*(+180) + (215/216)*(-1) = -35/216 =-16.20%.
- Anytriplet:
There are 6 ways to rolla triplet. The player's edge is thus 6/216*(+30) +(210/216)*(-1) = -30/216 = -13.889%.
- Specificpair:
Lets assume the pair chosen is ones. There are 16 ways two or three of thatnumber can be rolled: 1+1+1, 1+1+2 * 3 ways, 1+1+3 * 3 ways, 1+1+4 * 3 ways, 1+1+5 * 3 ways, 1+1+6 * 3 ways. Theplayer's edge is thus 16/216*(+10) + (200/216)*(-1) = -72/216 = -18.52%.
Following is a formula for s spots over n dice, taken from The Theory of Gambling and Statistical Logic by Richard A. Epstein, formula 5-14.
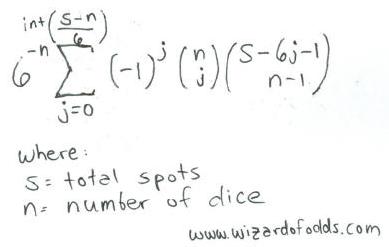
For example, let's look at the number of ways to get 11 spots over 3 dice.
int[(s-n)/6] = int[(11-3)/6] = int[1.33] = 1
The total would be 6-3 * [-10*combin(3,0)*combin(11-6*0-1,3-1) + -11*combin(3,1)*combin(11-6*1-1,3-1) ] =
1/216 * [1*1*combin(10,2) + -1*3*combin(4,2)] =
1/216 * [1*1*45 + -1*3*6] =
1/216 * [45-18] = 27/216 = 12.5%



