On this page
Obscure Topics in Betting Major League Baseball
Introduction
This page is meant as an appendix to my main page on Betting Major League Baseball. When I created that page it was based on data from the 2000 to 2009 seasons. In September 2018 I updated it based on the 2016 and 2017 seasons. However, there were some obscure tables I didn't bother to update. I put too much time into them to just throw them away, so copied and pasted the content off to this page.
Source of Data
The data this analysis is based on is from the Major League Baseball games played over the 2000 to 2009 seasons. I had to remove some games because of incomplete or corrupt data.
Run Line Bets
Unfortunately, my data does not indicate the run line bets. However, I can offer the following tables to help determine the fair run line according to the fair money line (F.M.L.) and total. I used logistic regression to create these tables, which was no easy task.
The first table is for away underdogs +1.5 runs. To get the fair money line the other way, on a home favorite -1.5 runs, take the opposite line by multiplying by -1.
Fair Run Lines for Away Underdogs +1.5
| F.M.L. | Total | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 7 | 7.5 | 8 | 8.5 | 9 | 9.5 | 10 | 10.5 | 11 | 11.5 | 12 | |
| 100 | -212 | -207 | -203 | -199 | -195 | -191 | -187 | -183 | -180 | -176 | -173 |
| 105 | -203 | -199 | -195 | -191 | -187 | -183 | -179 | -176 | -172 | -169 | -165 |
| 110 | -195 | -191 | -187 | -183 | -180 | -176 | -172 | -169 | -165 | -162 | -159 |
| 115 | -188 | -184 | -180 | -176 | -173 | -169 | -166 | -163 | -159 | -156 | -153 |
| 120 | -181 | -177 | -174 | -170 | -167 | -163 | -160 | -157 | -154 | -150 | -147 |
| 125 | -175 | -171 | -168 | -164 | -161 | -158 | -154 | -151 | -148 | -145 | -142 |
| 130 | -169 | -165 | -162 | -159 | -156 | -152 | -149 | -146 | -143 | -140 | -138 |
| 135 | -164 | -160 | -157 | -154 | -151 | -148 | -145 | -142 | -139 | -136 | -133 |
| 140 | -159 | -155 | -152 | -149 | -146 | -143 | -140 | -137 | -135 | -132 | -129 |
| 145 | -154 | -151 | -148 | -145 | -142 | -139 | -136 | -133 | -131 | -128 | -125 |
| 150 | -150 | -147 | -144 | -141 | -138 | -135 | -132 | -130 | -127 | -124 | -122 |
| 155 | -146 | -143 | -140 | -137 | -134 | -131 | -129 | -126 | -124 | -121 | -119 |
| 160 | -142 | -139 | -136 | -133 | -131 | -128 | -125 | -123 | -120 | -118 | -116 |
| 165 | -138 | -136 | -133 | -130 | -127 | -125 | -122 | -120 | -117 | -115 | -113 |
| 170 | -135 | -132 | -130 | -127 | -124 | -122 | -119 | -117 | -115 | -112 | -110 |
| 175 | -132 | -129 | -127 | -124 | -122 | -119 | -117 | -114 | -112 | -110 | -108 |
| 180 | -129 | -126 | -124 | -121 | -119 | -116 | -114 | -112 | -109 | -107 | -105 |
| 185 | -126 | -124 | -121 | -119 | -116 | -114 | -112 | -109 | -107 | -105 | -103 |
| 190 | -124 | -121 | -119 | -116 | -114 | -112 | -109 | -107 | -105 | -103 | -101 |
| 195 | -121 | -119 | -116 | -114 | -112 | -109 | -107 | -105 | -103 | -101 | 101 |
| 200 | -119 | -116 | -114 | -112 | -109 | -107 | -105 | -103 | -101 | 101 | 103 |
| 210 | -114 | -112 | -110 | -108 | -105 | -103 | -101 | 101 | 103 | 105 | 107 |
| 220 | -110 | -108 | -106 | -104 | -102 | 100 | 102 | 104 | 107 | 109 | 111 |
| 230 | -107 | -105 | -103 | -101 | 102 | 104 | 106 | 108 | 110 | 112 | 115 |
| 240 | -104 | -102 | 101 | 103 | 105 | 107 | 109 | 111 | 114 | 116 | 118 |
| 250 | -101 | 101 | 103 | 106 | 108 | 110 | 112 | 115 | 117 | 119 | 122 |
| 260 | 102 | 104 | 106 | 109 | 111 | 113 | 115 | 118 | 120 | 123 | 125 |
| 270 | 105 | 107 | 109 | 111 | 114 | 116 | 118 | 121 | 123 | 126 | 129 |
| 280 | 107 | 110 | 112 | 114 | 117 | 119 | 121 | 124 | 127 | 129 | 132 |
| 290 | 110 | 112 | 115 | 117 | 119 | 122 | 124 | 127 | 130 | 132 | 135 |
| 300 | 112 | 115 | 117 | 120 | 122 | 125 | 127 | 130 | 132 | 135 | 138 |
| 310 | 115 | 117 | 120 | 122 | 125 | 127 | 130 | 133 | 135 | 138 | 141 |
| 320 | 117 | 120 | 122 | 125 | 127 | 130 | 132 | 135 | 138 | 141 | 144 |
| 330 | 119 | 122 | 124 | 127 | 130 | 132 | 135 | 138 | 141 | 144 | 147 |
| 340 | 122 | 124 | 127 | 129 | 132 | 135 | 138 | 140 | 143 | 146 | 149 |
| 350 | 124 | 126 | 129 | 132 | 134 | 137 | 140 | 143 | 146 | 149 | 152 |
| 360 | 126 | 128 | 131 | 134 | 137 | 139 | 142 | 145 | 148 | 151 | 154 |
| 370 | 128 | 131 | 133 | 136 | 139 | 142 | 145 | 148 | 151 | 154 | 157 |
| 380 | 130 | 133 | 135 | 138 | 141 | 144 | 147 | 150 | 153 | 156 | 159 |
| 390 | 132 | 135 | 137 | 140 | 143 | 146 | 149 | 152 | 155 | 159 | 162 |
| 400 | 134 | 136 | 139 | 142 | 145 | 148 | 151 | 154 | 158 | 161 | 164 |
Let's take a look at an example to see how to use the table. On April 6, 2010, the Las Vegas Hilton offered the following bets on the Yankees vs. Red Sox game. As always, the home team is listed last.
Yankees vs. Red Sox
| Team | Money Line | Total | Run Line |
|---|---|---|---|
| Yankees | 125 | 9.5 | -170 |
| Red Sox | -135 | 150 |
The fair line on the Yankees would be +130, which can be found by splitting the juice between the two teams. Next, look up the value in the table for +130 and 9.5, which is -152. So fair run line bets would be:
Yankees +1.5 -152
Red Sox -1.5 +152
The actual run lines are -170 and +150. Assuming my analysis was correct, the house edge on the Yankees run line would be 4.20% and on the Red Sox it would be 0.79%.
By the way, the actual score of the game was Yankees 6, Red Sox 4.
The next table shows the fair run lines for home underdogs. The reason for the significant difference between it and the away underdog table above is because it is more valuable to get the extra 1.5 runs on an away team. This is because the game will be over after any winning play by the home team in the 9th or later inning. Thus, there are a lot of games where the home team wins by one run.
Fair Run Lines for Home Underdogs +1.5
| F.M.L. | Total | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 7 | 7.5 | 8 | 8.5 | 9 | 9.5 | 10 | 10.5 | 11 | 11.5 | 12 | |
| 100 | -171 | -169 | -168 | -166 | -165 | -163 | -162 | -160 | -159 | -157 | -156 |
| 105 | -164 | -162 | -161 | -159 | -158 | -156 | -155 | -153 | -152 | -150 | -149 |
| 110 | -157 | -156 | -154 | -153 | -151 | -150 | -148 | -147 | -146 | -144 | -143 |
| 115 | -151 | -150 | -148 | -147 | -145 | -144 | -143 | -141 | -140 | -139 | -137 |
| 120 | -145 | -144 | -143 | -141 | -140 | -139 | -137 | -136 | -135 | -134 | -132 |
| 125 | -140 | -139 | -138 | -136 | -135 | -134 | -133 | -131 | -130 | -129 | -128 |
| 130 | -136 | -134 | -133 | -132 | -130 | -129 | -128 | -127 | -126 | -124 | -123 |
| 135 | -131 | -130 | -129 | -127 | -126 | -125 | -124 | -123 | -122 | -120 | -119 |
| 140 | -127 | -126 | -125 | -123 | -122 | -121 | -120 | -119 | -118 | -117 | -116 |
| 145 | -123 | -122 | -121 | -120 | -119 | -118 | -116 | -115 | -114 | -113 | -112 |
| 150 | -120 | -119 | -117 | -116 | -115 | -114 | -113 | -112 | -111 | -110 | -109 |
| 155 | -116 | -115 | -114 | -113 | -112 | -111 | -110 | -109 | -108 | -107 | -106 |
| 160 | -113 | -112 | -111 | -110 | -109 | -108 | -107 | -106 | -105 | -104 | -103 |
| 165 | -110 | -109 | -108 | -107 | -106 | -105 | -104 | -103 | -102 | -101 | -100 |
| 170 | -108 | -107 | -106 | -105 | -104 | -103 | -102 | -101 | 100 | 101 | 102 |
| 175 | -105 | -104 | -103 | -102 | -101 | -100 | 101 | 102 | 103 | 104 | 105 |
| 180 | -103 | -102 | -101 | 100 | 101 | 102 | 103 | 104 | 105 | 106 | 107 |
| 185 | -100 | 100 | 101 | 102 | 103 | 104 | 105 | 106 | 107 | 108 | 109 |
| 190 | 102 | 103 | 104 | 105 | 106 | 107 | 108 | 109 | 110 | 111 | 112 |
| 195 | 104 | 105 | 106 | 107 | 108 | 109 | 110 | 111 | 112 | 113 | 114 |
| 200 | 106 | 107 | 108 | 109 | 110 | 111 | 112 | 113 | 114 | 115 | 117 |
| 210 | 110 | 111 | 112 | 113 | 114 | 115 | 117 | 118 | 119 | 120 | 121 |
| 220 | 114 | 115 | 116 | 117 | 119 | 120 | 121 | 122 | 123 | 124 | 126 |
| 230 | 118 | 119 | 120 | 121 | 123 | 124 | 125 | 126 | 127 | 129 | 130 |
| 240 | 122 | 123 | 124 | 125 | 127 | 128 | 129 | 130 | 132 | 133 | 134 |
| 250 | 126 | 127 | 128 | 129 | 130 | 132 | 133 | 134 | 136 | 137 | 138 |
| 260 | 129 | 130 | 132 | 133 | 134 | 136 | 137 | 138 | 139 | 141 | 142 |
| 270 | 133 | 134 | 135 | 137 | 138 | 139 | 141 | 142 | 143 | 145 | 146 |
| 280 | 136 | 137 | 139 | 140 | 141 | 143 | 144 | 145 | 147 | 148 | 150 |
| 290 | 139 | 141 | 142 | 143 | 145 | 146 | 148 | 149 | 150 | 152 | 153 |
| 300 | 143 | 144 | 145 | 147 | 148 | 150 | 151 | 152 | 154 | 155 | 157 |
| 310 | 146 | 147 | 149 | 150 | 151 | 153 | 154 | 156 | 157 | 159 | 160 |
| 320 | 149 | 150 | 152 | 153 | 155 | 156 | 158 | 159 | 161 | 162 | 164 |
| 330 | 152 | 153 | 155 | 156 | 158 | 159 | 161 | 162 | 164 | 165 | 167 |
| 340 | 155 | 156 | 158 | 159 | 161 | 162 | 164 | 165 | 167 | 169 | 170 |
| 350 | 158 | 159 | 161 | 162 | 164 | 165 | 167 | 168 | 170 | 172 | 173 |
| 360 | 160 | 162 | 163 | 165 | 167 | 168 | 170 | 171 | 173 | 175 | 176 |
| 370 | 163 | 165 | 166 | 168 | 169 | 171 | 173 | 174 | 176 | 178 | 179 |
| 380 | 166 | 167 | 169 | 170 | 172 | 174 | 175 | 177 | 179 | 180 | 182 |
| 390 | 168 | 170 | 171 | 173 | 175 | 176 | 178 | 180 | 181 | 183 | 185 |
| 400 | 171 | 172 | 174 | 175 | 177 | 179 | 181 | 182 | 184 | 186 | 188 |
Alternate Totals
It often happens when you want to make an over or under bet in baseball that there are two different totals available. For example, 7.5 and 8. Of course, you have to pay a higher price if you want the half point to work in your favor. The price will depend on whether you are buying or selling an odd or an even number, because in baseball, odd totals are more common than even ones. During the zeros decade (somebody please come up with a term for it), 59.2% of Major League Baseball games ended in an odd total. Hopefully I don't need to explain why. The following tables shows the fair equivalent price to pay for buying an extra half point off either an over or under bet.
To use the table, look up the line on the lower of the two lines if betting the under, and the higher if betting the over. Whether you use the second or third column will depend on whether you're looking at an over or under bet, and whether the base line is odd, even, odd +0.5, or even +0.5. To be specific, if you're interested in the under, use the second column for an odd or even +0.5 base number, otherwise use the third column. If you're interested in the over, use the second column for an odd or odd +0.5 base number, otherwise use the third column.
Alternative Totals for Buying a Half Point
| Market Line | Off the Under | |
|---|---|---|
| Odd, Even +0.5 | Even, Odd +0.5 | |
| Off the Over | ||
| Odd or Odd +0.5 | Even or Even +0.5 | |
| -140 | -177 | -165 |
| -135 | -170 | -159 |
| -130 | -164 | -153 |
| -125 | -157 | -147 |
| -120 | -151 | -141 |
| -115 | -144 | -135 |
| -110 | -138 | -129 |
| -105 | -131 | -123 |
| 100 | -125 | -117 |
| 105 | -119 | -111 |
| 110 | -114 | -106 |
| 115 | -109 | -102 |
| 120 | -104 | 103 |
| 125 | -100 | 107 |
| 130 | 104 | 111 |
| 135 | 108 | 115 |
| 140 | 112 | 119 |
Let's look at an example of how to use the table. In the Astros vs. Marlins game today (Aug. 20, 2010) as I write this, you can get under 7.5 at the Hilton for -105 or under 8 at the MGM for -135. Which is the better bet? 7.5 is an "odd +0.5" number. The -105 row and the "even, odd +0.5" column meet at -123. That means you should be indifferent between betting under 7.5 -105 and under 8 -123. The actual MGM price was -135, so in this example the under 7.5 -105 at the Hilton is the better bet.
The next table shows the fair price to pay if you want to buy a half point off of an over bet. For example, in the same Astros vs. Marlins game, you can bet over 7.5 at -115 at the Hilton or over 8 at +115 at the MGM. Which is the better bet? We should use 8 as the base line, because the alterative of 7.5 is a half-point better. So looking at the +115 row and the "even or even +0.5" column we see the fair equivalent is -102. The Hilton price on over 7.5 is -115, which is worse than -102, making over 8 +115 at the MGM the better bet.
Let's look at some more examples. Here are some lines from the Braves Vs. Cubs game.
Hilton: Over 10 -115, Under 10 -105
MGM: Over 10.5 EV, Under 10.5 -120
If we assume under 10 -105 to be fair, then the equivalent bet is under 10.5 -123. So the under 10.5 -120 at the MGM is better. If we assume over 10.5 EV to be fair, then the equivalent bet is over 10 -117. So the over 10 -115 at the Hilton is better.
Next, here are lines from the Bluejays vs Red Sox game.
Stations: Over 8.5 -105, Under 8.5 -115
Hilton: Over 8 -125, Under 8 +105
If we assume under 8 +105 to be fair, then the equivalent bet is under 8.5 -111. The under 8.5 -115 at Stations is not as good, so under 8 +105 is the better bet. If we assume over 8.5 -105 to be fair, then the equivalent bet is over 8 -123. The over 8 -125 at the Hilton is not as good, so the over 8 -105 is the better bet.
Total Runs, Hits, and Errors
Sometimes in the post-season, the casinos will offer an over/under prop on the total combined runs, hits and errors. I noticed there is a fairly linear relationship between the projected total and the actual total of runs, hits and errors. The least-squares regression line for the estimated total runs, hits and errors is 12.45 + 1.817 × t, where t represented the estimated total.
The following table shows the estimated and actual total runs, hits and errors according to the projected total runs.
Total Combined Runs, Hits and Errors in MLB
| Total | Sample Size | Estimated | Actual |
|---|---|---|---|
| 6 | 1 | 23.35 | 14.00 |
| 6.5 | 71 | 24.26 | 24.46 |
| 7 | 610 | 25.17 | 24.81 |
| 7.5 | 1635 | 26.08 | 26.36 |
| 8 | 2393 | 26.98 | 26.74 |
| 8.5 | 4122 | 27.89 | 27.80 |
| 9 | 5337 | 28.80 | 28.88 |
| 9.5 | 4472 | 29.71 | 29.92 |
| 10 | 2395 | 30.62 | 30.53 |
| 10.5 | 1736 | 31.53 | 31.42 |
| 11 | 747 | 32.43 | 32.22 |
| 11.5 | 285 | 33.34 | 33.75 |
| 12 | 131 | 34.25 | 33.80 |
| 12.5 | 102 | 35.16 | 33.61 |
| 13 | 77 | 36.07 | 35.97 |
| 13.5 | 55 | 36.98 | 36.73 |
| 14 | 47 | 37.89 | 35.96 |
| 14.5 | 35 | 38.79 | 40.29 |
| 15 | 15 | 39.70 | 45.33 |
Run Scored in First Inning
A popular proposition bet in baseball is whether or not a run will be scored in the first inning. It is pretty obvious that the probability of a run in the first inning would be highly correlated to the projected total. The following table shows the number of games with a run in the first inning, according to the total. The second column, titled RSFI, stands for "Run Scored in the First Inning." This table was based on the 2001 to 2011 seasons. The lower right cell shows an overall probability of at least one run in the first inning of 52.5%.
Run Scored in First Inning Data
| Total | RSFI | Total Games | Ratio |
|---|---|---|---|
| 5 | 0 | 1 | 0.00% |
| 5.5 | 13 | 17 | 76.47% |
| 6 | 30 | 68 | 44.12% |
| 6.5 | 134 | 335 | 40.00% |
| 7 | 537 | 1127 | 47.65% |
| 7.5 | 1093 | 2313 | 47.25% |
| 8 | 1544 | 3109 | 49.66% |
| 8.5 | 2603 | 5039 | 51.66% |
| 9 | 3054 | 5859 | 52.12% |
| 9.5 | 2415 | 4403 | 54.85% |
| 10 | 1199 | 2163 | 55.43% |
| 10.5 | 811 | 1358 | 59.72% |
| 11 | 313 | 516 | 60.66% |
| 11.5 | 128 | 206 | 62.14% |
| 12 | 72 | 112 | 64.29% |
| 12.5 | 64 | 103 | 62.14% |
| 13 | 47 | 68 | 69.12% |
| 13.5 | 26 | 41 | 63.41% |
| 14 | 10 | 16 | 62.50% |
| 14.5 | 8 | 12 | 66.67% |
| 15 | 1 | 1 | 100.00% |
| Total | 14102 | 26867 | 52.49% |
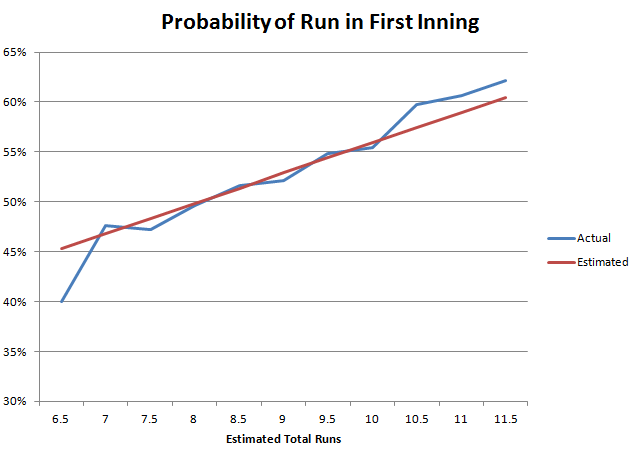
Here is what that looks like in a graph. The blue line shows the actual percentage of games with a run in the first inning by estimated total runs, from 6.5 to 11.5. The red line is called a "least-squared" regression line, which smooths out the ups and downs by showing the line that best matches the game total to the probability of a first-inning run. The equation for that line is p=0.2554 + 0.0304×t, where p = probability of first-inning run, and t=estimated total runs.
I also considered whether it mattered if the game had a big favorite. Given the same total, I found that that money lines on the game didn't affect the probability of a first-inning run.
In baseball, the odds are often different depending on whether a bet is on the under or over the projected total runs. For example, in a game on April 13, 2012, between the Brewers and Braves the total is 7.5. At Bovada, the line on the over is -125, and on the under is +105. Given the pressure on a high total, that would indicate an increased probability of a run in the first inning. What I suggest to adjust for that is to use the following modified formula when there is unequal demand between the over and under.
p = 0.2554 + 0.0304×t + 0.000724×f, where
p = Probability of first-inning run
t = Projected game total
f = Favoritism points on the over
Let me explain "favoritism points on the over." This is how many point the money line on the over has moved in the direction of the over being the favorite side. For example, if the sports book has a 20-cent line on the total, meaning the under and over are 20 points apart, then the following table shows the number "favoritism points on the over."
Favoritism Points on the Over
| Money Line on Over |
Favoritism Points |
|---|---|
| 130 | -40 |
| 125 | -35 |
| 120 | -30 |
| 115 | -25 |
| 110 | -20 |
| 105 | -15 |
| 100 | -10 |
| -105 | -5 |
| -110 | 0 |
| -115 | 5 |
| -120 | 10 |
| -125 | 15 |
| -130 | 20 |
| -135 | 25 |
| -140 | 30 |
| -145 | 35 |
| -150 | 40 |
Let's look at a couple of examples, based on a 20-cent total.
Example 1: Mets vs. Phillies, over 6.5 -115. The table above shows 5 favoritism points. So the probability of a run in the first inning is:
p = 0.2554 + 0.0304×6.5 + 0.000724×5 = 0.45662. That equates to a fair line on a first-inning run of +119.
Example 2: Orioles vs. Yankees, over 7.5 -105. The table above shows -5 favoritism points. So the probability of a run in the first inning is:
p = 0.2554 + 0.0304×7.5 + 0.000724×-5 = 0.47978. That equates to a fair line on a first-inning run of +108.
If you're using a sports book with other than a 20-cent line on the total, then adjust the favoritism points accordingly.
A look at actual lines on this prop shows that most sports books set them well enough to not find an advantage either way. However, I found one book that seemed to favor the "no" on this prop, often making betting on a first-inning run a good value. It is good to try to bet at such places early, to beat the other sharp bettors.




