On this page
Simple Strategy for Deuces Wild Video Poker
Introduction
The following strategy is my "simple strategy" for deuces wild video poker. Using the strategy on a full pay machine will result in an expected return of 100.71%. Compared to the optimal strategy return of 100.76%, mistakes in the simple strategy will cost 0.05%, or one total bet every 1869 hands.
To use the strategy look up all viable ways to play an initial hand on the following list and elect that which is highest on the list.
4 deuces- 4 deuces
- Pat royal flush
- 3 deuces only
- Any pat four of a kind or higher
- 4 to a royal flush
- 4 to a straight flush with 2 consecutive singletons, 6-7 or higher
- 2 deuces only
- Any pat four of a kind or higher
- 4 to a royal flush
- Full house
- 4 to a straight flush with 3 consecutive singletons, 5-7 or higher
- 3 of a kind, straight, or flush
- All other 4 to a straight flush
- 3 to a royal flush
- 3 to a straight flush with 2 consecutive singletons, 6-7 or higher
- deuce only
- 4,5 to a royal flush
- Made three of a kind to straight flush
- 4 to a straight flush
- 3 to a royal flush
- Pair
- 4 to a flush
- 4 to an outside straight
- 3 to a straight flush
- 4 to an inside straight, except missing deuce
- 2 to a royal flush, J,Q high
Outside straight: An open ended straight that can be completed at either end, such as the cards 7,8,9,10.
Inside straight: A straight with a missing inside card, such as the cards 6,7,9,10. In addition A,2,3,4 and J,Q,K,A also count as inside straights because they are at an extreme end.
Any hand that does not appear on the above lists should never be played. Most notably a two pair, keeping a single pair has a higher expected value.
Example: Suppose you have the following hand.

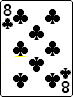
The top two plays are (1) keep the pat flush, and (2)keep the 4 to a straight flush. The 4 to a straight flush consists of 3 consecutive singletons with a range of 5-7 or greater. This appears higher on the list than a pat flush,and is thus the better play.
Comparison to Optimal Strategy
The following table compares the probability and return of each hand under both the simple strategy and the optimal strategy.
Simple Strategy to Optimal Strategy Comparison
| Hand | Pays | Probability | |||
|---|---|---|---|---|---|
| Simple | Optimal | Simple | Optimal | ||
| Natural royal flush | 800 | 0.000022 | 0.000022 | 0.017396 | 0.017667 |
| 4 deuces | 200 | 0.000206 | 0.000204 | 0.041257 | 0.040741 |
| Wild royal flush | 25 | 0.001785 | 0.001796 | 0.044631 | 0.044896 |
| 5 of a kind | 15 | 0.003164 | 0.003202 | 0.047466 | 0.048024 |
| Straight flush | 9 | 0.004206 | 0.00412 | 0.037854 | 0.037079 |
| 4 of a kind | 5 | 0.06523 | 0.064938 | 0.326151 | 0.324691 |
| Full house | 3 | 0.021303 | 0.021229 | 0.063909 | 0.063687 |
| Flush | 2 | 0.016977 | 0.016581 | 0.033955 | 0.033161 |
| Straight | 2 | 0.053711 | 0.056564 | 0.107422 | 0.113129 |
| 3 of a kind | 1 | 0.287044 | 0.284544 | 0.287044 | 0.284544 |
| Nothing | 0 | 0.546351 | 0.5468 | 0 | 0 |
| Total | 1 | 1 | 1.007085 | 1.00762 | |
The next table is a frequency distribution of the error, or difference in expected return, between the simple strategy and the optimal strategy.
Error Frequency
| Error | Number | Probability |
|---|---|---|
| 0 | 2520216 | 0.969702 |
| .01%-0.99% | 16488 | 0.006344 |
| 1.00%-1.99% | 37848 | 0.014563 |
| 2.00%-2.99% | 18336 | 0.007055 |
| 3.00%-3.99% | 1548 | 0.000596 |
| 4.00%-4.99% | 492 | 0.000189 |
| 5.00%-5.99% | 2700 | 0.001039 |
| 6.00%-6.99% | 864 | 0.000332 |
| 7.00%-7.99% | 180 | 0.000069 |
| 8.00%-8.99% | 252 | 0.000097 |
| 9.00%-9.99% | 0 | 0 |
| 10.00%-10.99% | 36 | 0.000014 |
| Total | 2598960 | 1 |







