On this page
Flip & Pay Poker
Introduction
Flip & Pay Poker is a video poker variant that is placed on top of conventional video poker games, single-line or multi-line. The player can play those games normally or pay a fee equal to the maximum bet amount of five coins per line to invoke the Flip & Pay feature. If the feature is active, cards may flip a card one rank in either direction, leaving the suit the same, if it improves the hand to at least a two pair.
Rules
- Flip & Pay can play like conventional three-, five-, or ten-play video poker. In addition, if the player pays a fee equal to the total bet amount if playing without the feature, then he will invoke the Flip & Pay feature.
- With the feature active, at most one card will flip one position in rank, but not suit, on the deal if these conditions are bet:
- The flip results in a hand of two pair or higher.
- The flip results in a hand of greater expected value than with the original card.
- The flip results in a card not already in the player's hand.
- The flip improves the hand on the deal by at least one level. For example, a pair to a three of a kind.
- If more than one card meet these requirements, the game will chose the flip that results in a hand of the greatest expected value.
- Cards of rank three to king can flip one rank in either direction. For example, the seven of hearts can flip to the six of hearts or eight of hearts.
- The deuce can flip to a three or ace.
- The ace can flip to a deuce or king.
- The player can choose to un-flip the card if he wants, but he never should.
- If a card gets flipped, the old card will be put back in the deck, available to get on the draw.
- In addition to the enabling the feature, the additional fee pumps up the pay table, generally on the straight, flush, and full house.
Example
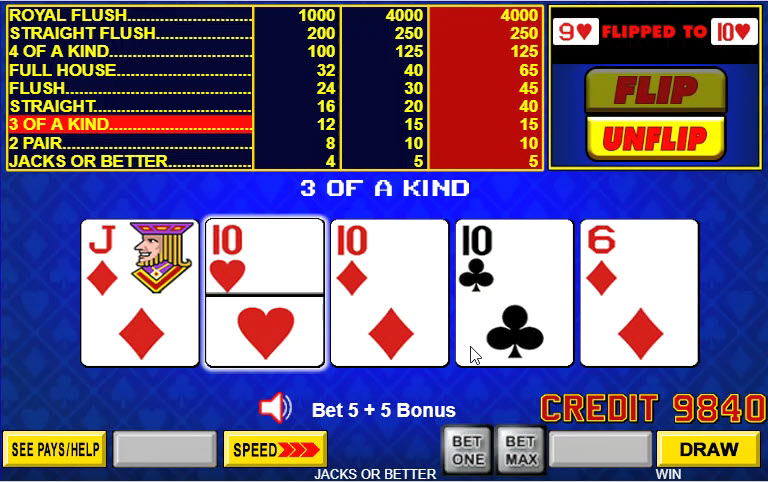
In the hand above I was initially dealt a 9 of hearts in the second position from the left. Increasing the rank by one improved what would have been a pair of tens to three tens.
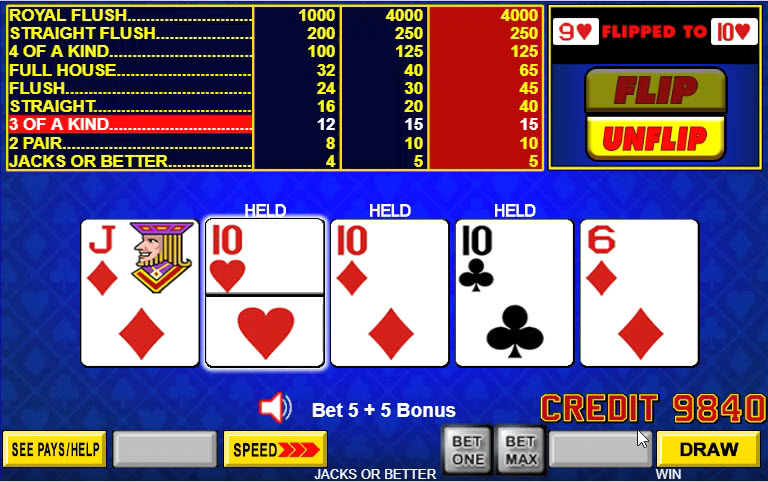
In the image above, I hold the three tens and discard the jack and six. Since I accepted the flip, the 9 of hearts is returned to the deck.

On the draw, I get the 10 of spades, improving my hand to four tens, paying 125 credits.
Analysis
Action Gaming Return Table
The following table shows all games, pay tables, and returns available for Flip & Play. This information was kindly provided by Action Gaming. Please remember my returns are slightly higher. The table shows both the pay table and return for the base game, based on a five-coin bet, and the pay table and return with the feature.
Action Gaming Return Table
| Game | Base Game Pay Table |
Feature Pay Table |
Base Game Return |
Feature Return |
|---|---|---|---|---|
| Double Double Bonus | 9-5 | 12-6 | 97.87% | 99.84% |
| Double Double Bonus | 8-5 | 11-6 | 96.79% | 98.29% |
| Double Double Bonus | 7-5 | 10-6 | 95.71% | 96.75% |
| Double Double Bonus | 6-5 | 9-6 | 94.66% | 95.21% |
| Triple Double Bonus | 8-5-4 | 8-5-4 | 95.97% | 99.23% |
| Triple Double Bonus | 7-5-4 | 7-5-4 | 94.92% | 97.82% |
| Triple Double Bonus | 6-5-4 | 6-5-4 | 93.87% | 96.40% |
| Triple Double Bonus | 6-5-3 | 6-5-3 | 92.65% | 95.11% |
| Bonus Poker | 8-5-4 | 13-9-7 | 99.17% | 99.89% |
| Bonus Poker | 7-5-4 | 12-9-7 | 98.01% | 98.21% |
| Bonus Poker | 6-5-4 | 11-10-7 | 96.87% | 97.35% |
| Bonus Poker | 6-5-3 | 11-9-7 | 95.78% | 96.53% |
| Bonus Poker | 10-8-5-3-1 | 13-10-7 | 94.18% | 95.31% |
| Double Bonus | 9-6-5 | 12-7-6 | 97.81% | 98.76% |
| Double Bonus | 9-6-4 | 12-7-5 | 96.38% | 97.21% |
| Double Bonus | 8-5-4 | 11-6-5 | 94.19% | 94.88% |
| Double Bonus | 7-5-4 | 11-6-5 | 93.11% | 93.86% |
| Jacks or Better | 8-6 | 13-9-8 | 98.39% | 98.56% |
| Jacks or Better | 8-5 | 13-10-7 | 97.30% | 97.63% |
| Jacks or Better | 7-5 | 12-9-8 | 96.15% | 96.87% |
| Jacks or Better | 6-5 | 11-9-8 | 95.00% | 95.19% |
| Bonus Deluxe | 8-6 | 10-7-5 | 98.49% | 99.46% |
| Bonus Deluxe | 8-5 | 9-8-5 | 97.40% | 98.55% |
| Bonus Deluxe | 7-5 | 9-6-5 | 96.25% | 97.13% |
| Bonus Deluxe | 6-5 | 8-7-5 | 95.36% | 96.06% |
External Links
- Flip & Pay Poker -- Discussion in my forum at Wizard of Vegas.
Acknowledgements
I would like to thank Gary J. Koehler for verifying the returns in the tables above.




