Folded Rectangle Puzzle
For this newsletter I present a math puzzle from the November issue of the Mensa Bulletin.
Consider a 1x4 rectangle. Now fold that rectangle so that opposite corners overlap, as in this diagram.
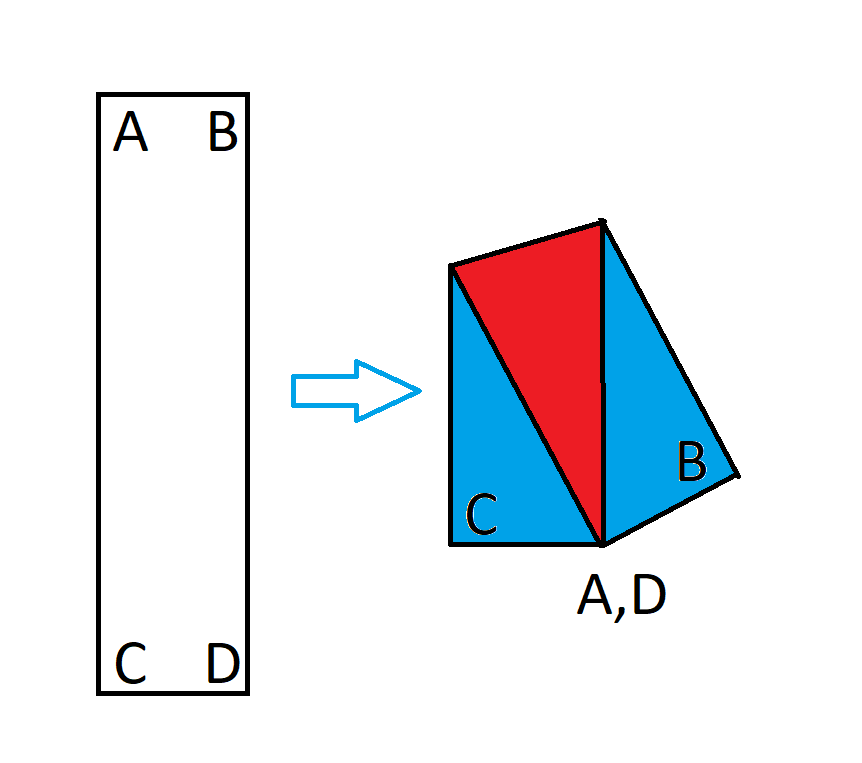
After the rectangle is folded it makes an irregular pentagon. What is the ratio of the portion of that pentagon where the paper overlaps to the total area? In other words, the ratio of the red area in the image above to the total area.
Scroll down for the answer and solution.
Answer
The answer is 17/47 = apx. 0.3617
Solution
To explain the solution, let me define some more points, as seen in the following image. F is the midpoint of E and G.
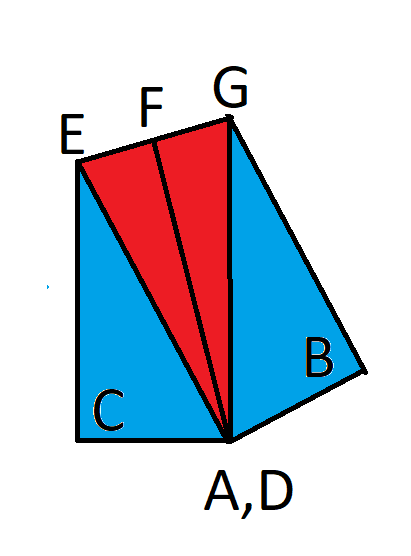
We know:
AC = 1
CE + AE = 4
Let’s solve for AE using the Pythagorean theorem:
12 + (CE)2 = (AE)2
Substituting 4 – CE for AE we get:
12 + (CE)2 = (4 – CE)2
1 + (CE)2 = 16 – 8(CE) + (CE)2
8(CE) = 15
CE = 15/8
Going back to 12 + (CE)2 = (AE)2, we can solve for (AE) since we know EC:
(AE)2 = (CE)2 + 12
(AE)2 = (15/8)2 + 12
(AE)2 = 225/64 + 64/64
(AE)2 = 289/64
AE = 17/8
Before the fold, the length from A to D was the diagonal of the rectangle. Using Pythagorean again, the length is sqrt(17).
(AF) is half that length, or sqrt(17)/2.
Knowing AE and AF, we can solve for EF using the Pythagorean again:
(AE)2 = (EF)2 + (AF)2
(17/8)2 = (EF)2 + (sqrt(17)/2)2
289/64 = (EF)2 + 17/4
289/64 = (EF)2 + 272/64
(EF)2 = 17/64
EF = sqrt(17)/8
As stated before, F is the midpoint of E and G. This EG = 2*sqrt(17)/8 = sqrt(17)/4.
The red triangle, AEG = (1/2) × base × height =
= (1/2) × sqrt(17/4) × sqrt(17)/2
= (1/2) × (17/8) = 17/16
The area of triangle ACE = (1/2)*base*height =
(1/2) × 1 × (15/8) = 15/16.
The area of the whole pentagon = AEG + 2*ACE =
(17/16) + 2*(15/16) = 47/16
Thus, the area of the red area to the entire pentagon =
(17/16) / (47/16) = 17/47 = apx. 0.3617




