Ask The Wizard #388

In this image, how much profit is the money changing business making?
For the benefit of others, let me explain the way to read the table. I assume this table is for how much the money exchanger is selling and buying foreign currencies relative to the Great British Pound (£), since that currency isn't listed. Let's look at the US dollar ($) numbers, for example. It is saying they will sell you £1 for $1.5085 and will sell you $1.2658 for £1 .
Assuming they make the same profit either way, the expected return, for lack of a better term, is the square root of the ratio of the smaller number to the larger number. In this case sqrt(1.2658/1.5085) = 91.60%. The difference from 100% is the money changer's profit, or the "house edge" to using a gambling term, which in this example is 8.40%.
Currency Exchange Expected Return and House Edge
| Country | Buy | Sell | Expected Return |
House Edge |
|---|---|---|---|---|
| Euro | 1.1800 | 0.9959 | 91.87% | 8.13% |
| USA | 1.5085 | 1.2658 | 91.60% | 8.40% |
| South Africa | 15.7723 | 12.3244 | 88.40% | 11.60% |
| Hong Kong | 11.6445 | 9.8024 | 91.75% | 8.25% |
| Japan | 134.6200 | 108.9200 | 89.95% | 10.05% |
| Australia | 2.3282 | 1.8738 | 89.71% | 10.29% |
| Canada | 1.8868 | 1.5510 | 90.67% | 9.33% |
| Switzerland | 1.8179 | 1.4372 | 88.91% | 11.09% |
| UAE | 5.5920 | 4.4792 | 89.50% | 10.50% |
| Saudi Arabia | 5.8807 | 4.5588 | 88.05% | 11.95% |
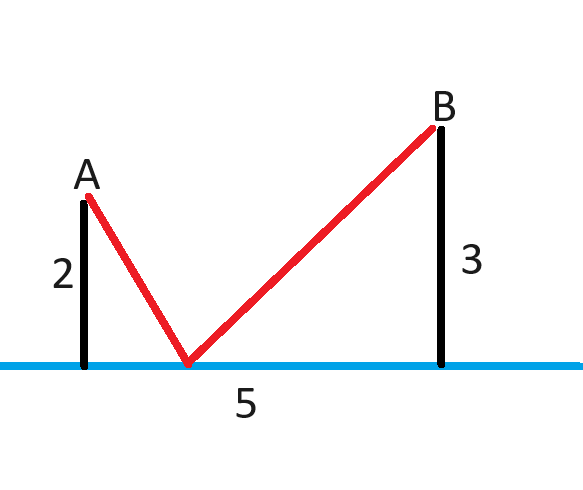
There is a straight water pipe (blue) in the vicinity of points A and B. Point A is 2 miles from the closest point on the pipe. Point B is 3 miles from the closest point on the pipe. The two points along the pipe that mark the closest points to A and B are 5 miles apart. It is desired to lay two new pipes (red), linking A and B to the water-bearing pipe, having only one point of contact with the water pipe with the two new pipes going directly to A and B. In other words, the new pipes must form a V shape. What is the least distance of pipe required?
Here is my solution (PDF)
There is a straight water pipe (blue) in the vicinity of points A and B. Point A is 2 miles from the closest point on the pipe. Point B is 3 miles from the closest point on the pipe. These two points along the pipe that mark the closest points to A and B are 5 miles apart. It is desired to provide water to points A and B by laying new pipes linking points A and B to anywhere along the blue pipe. These new pipes may be in any form you wish. What is the least distance of new pipe needed?
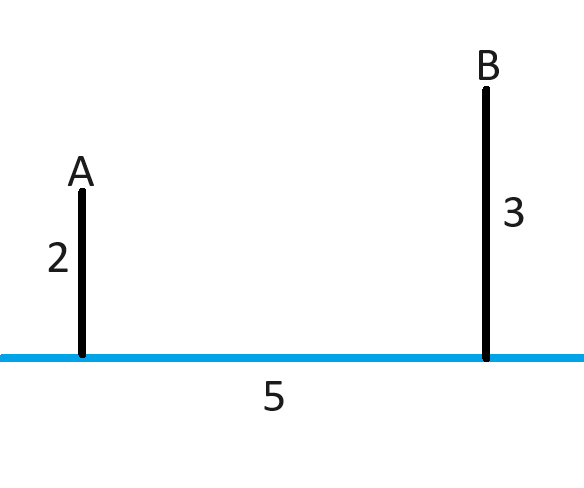
The new pipes should form a Y shape, with one end leading to the existing water pipe and the other two ends leading to the two houses.
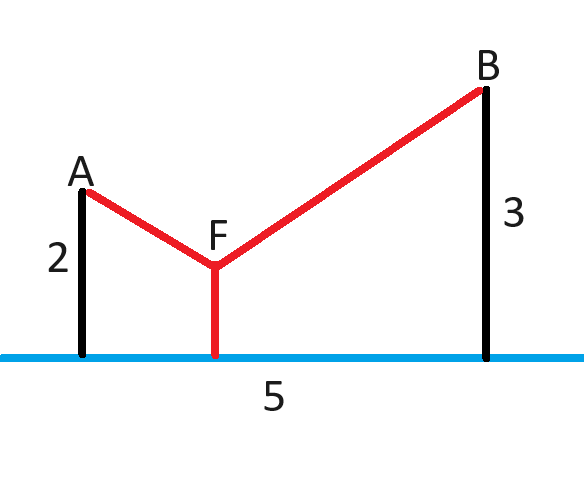
The point in (or in some cases out) of a triangle that minimizes the sum of the distances to each vertex is called the Fermat Point. I won't get into how to find it, but a property is that the lines it makes to the three vertexes form three 120° angles.

For more information, see the Wikipedia entry on the Fermat Point.
Here is my solution (PDF).




