Ask The Wizard #391
12 + 22 + 32 + ... + n2 = ?
Suppose you flip a fair coin one million times. Using only a simple calculator with the five basic arithmetic functions (+,0,*,/,^) , what is the probability of getting exactly the same number of heads and tails? A close estimate will suffice.
Recall the equation for the standard normal curve:
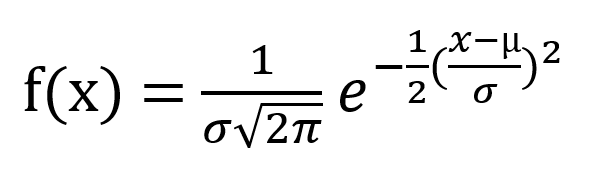
The expected number of tails in one flip is 0.5 and the expected squared number of tails is also 0.5. Thus, the variance of the number of tails in one flip is 0.5-(0.5)2 = 0.5 - 0.25 = 0.25. The variance of one million flips is 1,000,000 * 0.25 = 250,000. The standard deviation of one million flips is the square root of that: sqrt(250,000) = 5,000.
Let x = the number of tails over the expected number of 500,000. The mean of x is zero. As shown, the standard deviation of x is 5,000.
The probability of x=0 is thus:
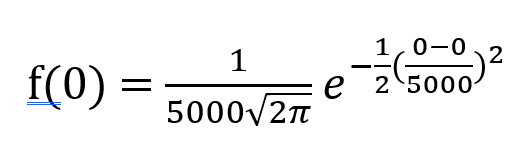
This simplifies to 1/(5000*sqrt(2*π)) =~ 0.000797885 =~ 1 in 1253.314137.
Links
Wikipedia entry on the standard normal curve.
You are riding a bicycle down an exercise path at 15 mph. On the path are joggers going at 5 mph. There are an equal number of joggers going in each direction. What ratio of joggers you pass will be going in the opposite direction as you?
Assume the path to be 15 miles long.
The bicyclist would encounter joggers who started from the other side anywhere from 3 hours before I started to 1 hour after, for a total of 4 hours of joggers encountered.
Going the same direction, the bicyclist would encounter joggers who left anywhere from 2 hours before me to the same time, for a total of 2 hours.
Thus, twice as many joggers would be going in the opposite direction. The ratio of joggers going the opposite way to all joggers is 4/(2+4) = 2/3.
Relative to joggers going the same direction, your speed is 15-5 = 10 mph.
Relative to joggers going the opposite direction, your speed is 15+5 = 20 mph.
So, you will pass twice as many joggers going the opposite direction. That results in a ratio of 2/(1+2) = 2/3.
This question is asked and discussed in my forum at Wizard of Vegas.




