Ask The Wizard #402
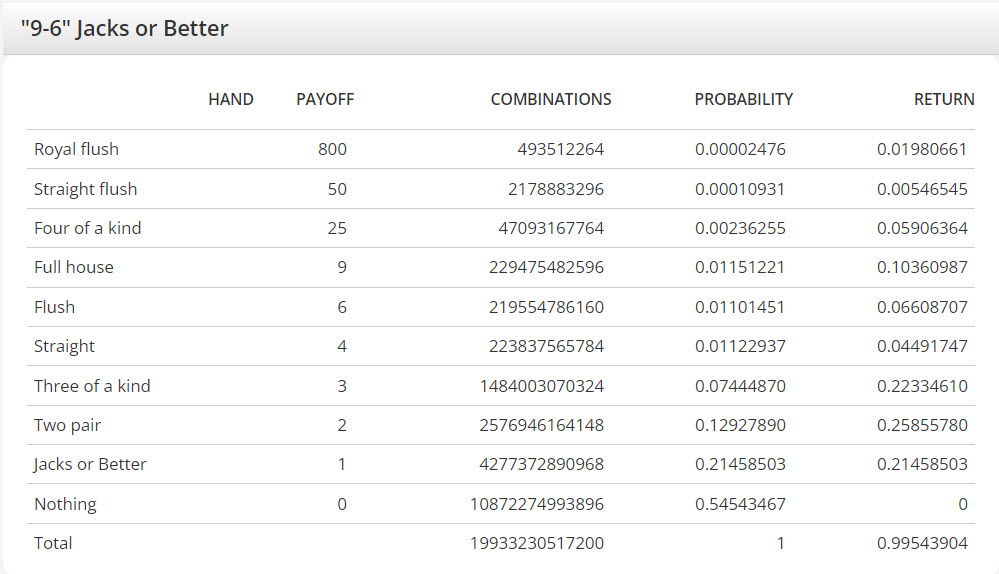
On your video poker calculator for 9-6 Jacks or Better your table sites 1,661,102,543,100 as the total number of combinations. Meanwhile, your Jacks or Better page sites 19,933,230,517,200 as the total number of combinations. It seems to me the number of combinations should be the same. I am wondering why the difference? The return (0.995439) appears to be the same.
Yes, the two sources address the same game.

The reason has to do with the way the game is analyzed. The more cards the player discards, the greater the number of combinations on the draw. The following table shows the number of combinations there are on the draw, which is the number of ways you can choose the number of discards among the 47 cards left in the deck.
| Discards | Combinations on Draw | Weighting |
| 0 | 1 | 7,669,695 |
| 1 | 47 | 163,185 |
| 2 | 1,081 | 7,095 |
| 3 | 16,215 | 473 |
| 4 | 178,365 | 43 |
| 5 | 1,533,939 | 5 |
The least common multiple of 1, 47, 1081, 16215, 178365 and 1533939 is 7669695.
It is important that each starting hand has the same total weighting. To achieve this, I apply a weighting factor to each hand, according to the number of discards. This weighting factor is in the right column of the table above. The product of the number of combinations on the draw and the weighting factor will always be 7,669,695.
There are a combin(52,5) = 52!/(47!*5!) = (48*49*50*51*52)/(1*2*3*4*5) = 2,598,960 ways to choose five cards out of 52. So, the total number of combinations in video poker the way I analyze it is combin(52,5)*combin(47,5)*5 = 2,598,960 * 7,669,695 = 19,933,230,517,200. That is why you see that number so often as the total combinations in my return tables.
Why does the calculator say 1,661,102,543,100 then, you might ask? Video poker programming genius JB did that calculator. He added a step to find the greatest common multiple of the combinations of each hand. This least common multiple was usually 12. Whatever it was, he divided each number of combinations by that least common multiple. I think it is because he likes to keep numbers as small as possible, while not sacrificing accuracy.
There is a one-meter rubber band, with an ant on one end. Each day the ant travels one centimeter. At the end of the day, the rubber band is expanded by one meter. How long will it take for the ant to reach the other side?
Fair warning that this is a rather difficult problem. In the spoiler box below I give a couple of hints to help you solve it.
Euler's Constant (not to be confused with Euler's number)
Here is my solution (PDF).
This question is asked and discussed in my forum at Wizard of Vegas.
My friend and I recently got two out of three Megabucks symbols. What are the odds of that?

According to my own page on Megabucks, the total weighting of each reel is 368, with the Megabucks symbols having a weighting of 1. So, the probability of any given reel landing on the Megabucks symbols is 1/368.
The probability of getting exactly 2 out of 3 is 3 × (1/368) * (1/368) × (367/368) =~ 0.0000220924 =~ in 1/45,264.




