Ask The Wizard #412
In baccarat, what is the probability one side (Banker or Player) will appear at least three times as much as the other in a shoe?
Please forgive me if I just do an estimate on this one.
The average shoe has 80.88 hands. On average, 7.70 will will be a tie, leaving 73.18 combined Banker and Player wins. For one side to have 3x as much as the other, it would need to occur 54.89 times and the other 18.30.
In 73.18 bets resolved, we can expect 37.09 Banker wins and 36.09 Player wins. One standard deviation on both is 4.28. To achieve 54.89 wins or more would be 4.16 standard deviations above expectations for the Banker and 4.39 for the Player. The probability of either side being this many standard deviations above expectations is about 1 in 47,000.
This question is asked and discussed in my forum at Wizard of Vegas.
The following are the betting odds for the winner of the 2028 presidential election. What is the probability anybody else wins?
| Bet | Pays |
|---|---|
| Vance | +250 |
| Newsom | +750 |
| Shapiro | +900 |
| M. Obama | +1200 |
| Buttigieg | +1400 |
| Whitmer | +1600 |
| Ramaswamy | +1600 |
| DeSantis | +2000 |
Futures bets like this tend to have a house edge of about 30%. If we added a hypothetical bet on the field at -160 odds, the overall set of bets would have a house edge of 29.95%. The following table shows the details. The "implied probability" shows the probability if the bet were exactly fair. The "actual probability" is the fair probability of each bet divided by the sum of the fair probabilities. This shows the probability of anyone else winning is 43.1%.
| Bet | Pays | Implied Probability |
Actual Probability |
|---|---|---|---|
| Vance | +250 | 0.285714 | 0.200136 |
| Newsom | +750 | 0.117647 | 0.082409 |
| Shapiro | +900 | 0.100000 | 0.070048 |
| M. Obama | +1200 | 0.076923 | 0.053883 |
| Buttigieg | +1400 | 0.066667 | 0.046698 |
| Whitmer | +1600 | 0.058824 | 0.041204 |
| Ramaswamy | +1600 | 0.058824 | 0.041204 |
| DeSantis | +2000 | 0.047619 | 0.033356 |
| Field | -160 | 0.615385 | 0.431062 |
| Total | 1.427602 | 1.000000 |
The overall return is the inverse of the sum of the implied probabilities, which is 1/1.427602 =~ 0.700475. The sum of the return and the house edge is 1, so the house edge is 1.000000 - 0.700475 = 0.299524.
This question is asked and discussed in my forum at Wizard of Vegas.
In the image below, the yellow circle has a radius of 1. What is the area of the red circle?
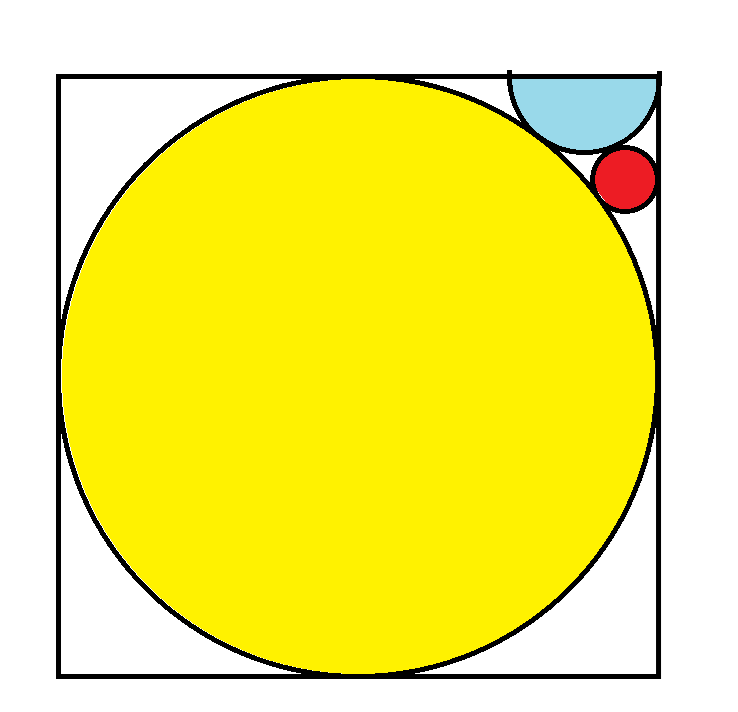
The answer is π/81 =~ 0.038785.
Here is my solution (PDF).
This question is asked and discussed in my forum at Wizard of Vegas.




