Texas Hold ’em - FAQ
Love your site, I have a math degree and I am a blackjack counter who has made numerous trips to Vegas and I want to start to use my math skills to play poker. I have watched poker from a distance in Vegas and would appreciate any advice/explanations of the rules of poker. Can I gain an advantage similar to counting in blackjack?
First, let me say that I'm not an expert on poker. It is no big secret that Texas Hold 'Em is the most popular form. In this game there are five community cards and only two down cards per player so a person good at calculating probabilities has more to go on. However, even the best math genius may make a bad poker player if he can't read the other players or the other players can easily read him (both of which I think are true in my case).
I have one simple question. I know you are the Wizard of odds but I need help. I play Craps and Texas Hold’em in the casinos. I fell I could be an intimidating force (THUS RAISING MY ODDS OF WINNING) if I could just figure out how to shuffle my poker chips. I have practiced but just can’t get it. I was hoping you could point me in a direction to learn this. Thank you for your time.
You asked the right person! I’m quite good at shuffling poker chips. Unfortunately I don’t often get to show it off because when I do play with chips it is usually counting cards or hole card reading, and in either case I don’t want to look like a pro. Anyway, start with a stack of 10 chips. Then cut them in half, putting two 5 stick chips side by side. Think of the two stacks as an 8. Put the 8 at about a 45 degree angle to your plane of symmetry. Put your thumb on the bottom of the 8, your index finger where the two stacks come together, and the other 3 fingers at the top of the 8. All five fingers should be barely touching the table. Then using your index finger gently lift both stacks while the other four fingers gently push the stacks together. After your index finger is about a quarter inch from the bottom of the table quickly move it away and keep pushing the stacks together with your other four fingers. It takes practice. I would recommend getting 10 nice clay chips and practicing at home or work. During commercials or whenever you have a minute to spare you can work on it. Before you know it you you’ll be riffling chips like a pro and casting fear in your fellow poker players.
How did you decide to simulate 5,197,920,000 games of 10-hands each for your Texas Hold’em page? Is that number significant?
I set my simulator to run a certain amount of time. Every 10,000 hands the program checks the time and when it has passed the ending time it stops wherever it is.
I'm glad to hear that you've gotten into playing Texas Hold 'em. I love the game and I'm winning online, but just barely. I've read more than a dozen books on Poker but I wanted to get your opinion on a couple of points
- How do you feel about "Position"? Example: Do you think there are really hands that are profitable from late position but should never be played from early position?
- What about "Pot Odds"? I understand the concept, but I've laid down a lot of hands that would have been winners, simply because I didn't have the correct odds to stay in and draw.... The charts on your website suggest that the strongest starting hands have a certain "Expected Value" if never folded. Do you recommend seeing these hands through to the river unless it's obvious that you're beaten (regardless of pot odds)?
Thank you for your time.
First, I'm still just a beginner so am not the best one to ask. Position is very important in hol 'em. The later your position the more information you have about your opponents' cards by the time it is your turn. For example if you pair the middle card on the flop, and it is check to you and you are last, then you can feel comfortable raising knowing that probably nobody paired the high card. However you'll see by the time the betting goes around the table. If you have a good, but not a great hand, and you raise it may get re-raised by players with stronger hands. If you check with such a hand it may check all the way around and you missed a chance to build up the pot and scare other players out. So don't just bet the value of your own cards, instead you have to weigh them against everyone else's cards. The later you are to play the more you will know about the other player's cards by the time it is your turn.
Pot odds is an important concept. As in any form of gambling the value of a bet depends on your probability of winning, the amount of the bet, and the amount of the win. The following table shows some common situations. The probability column shows the probability of making a straight or flush. The pot odds column shows the minimum number of bet units already in the pot for betting to be a good bet, assuming you will definitely win if you make your hand (unless you have the nut flush this is a big if).
Frequent Draws
| Hand | After | Probability of Making Hand |
Pot Odds |
|---|---|---|---|
| 4 to a flush | Flop | 34.97% | 1.86 |
| 4 to an outside straight | Flop | 31.45% | 2.18 |
| 4 to an inside straight | Flop | 16.47% | 5.07 |
| 4 to a flush | Turn | 19.57% | 4.11 |
| 4 to an outside straight | Turn | 17.39% | 4.75 |
| 4 to an inside straight | Turn | 8.70% | 10.50 |
There are lots of other factors to consider. One could write an entire book about it, and in fact many people have. Personally I recommend Get the Edge at Low-Limit Texas Hold 'em by Bill Burton as a introductory book on hold 'em. About my charts, no, definitely do not trust in a good starting hand the entire way through. There will be lots of times when you should fold a pair of aces. My tables are meant to only help the player bet before the flop. After the flop the expected value of your hand will likely change substantially.
When are you going to do something on bad beat jackpots?
I get asked about bad beat jackpots about once a month. When I have the time I plan to add a section to my site about it. My hesitation is I’ll get asked about every bad beat jackpot in every poker room in the whole world.
At a friendly home game of poker we were down to two players in a hand of Texas Hold ’em. I was out of the hand at looked at my neighbor’s cards. He was about to fold when I blurted out that he had a straight, which he obviously didn’t notice. The other player, with a weaker hand, said this was a breach of poker etiquette. Was he right?
Yes, he was. When playing poker if you are out of the hand, stay out. I don’t make an issue over players still in the game voluntarily showing their cards to other players, but I still don’t like it. However if you are out of the hand and see other cards you should keep your mouth shut. What is even more annoying is when somebody folds a hand and then proceeds to advise his girlfriend still in the hand. Offering advice is a major breach of etiquette if you are privy to information the player doesn’t have, namely the cards that you folded.
A Hold 'em tournament starts by high-carding for the button. Highest card wins, and spades beats hearts beats diamonds beats clubs. What is the average card that will win in a 10 person table? I've tried simulating it by assigning a number value to each card, but I can't figure it out for the life of me! Thanks and keep it up!
To simplify the question, let's say the cards were numbered 1 to 52. The following table shows the probability that the 10th to 52nd card is the highest card. There are combin(x-1,9) ways to choose 9 numbers under x and combin(52,10) ways to choose any number numbers out of 52. So the probability that x is the highest number can be expressed as combin(x-1,9)/combin(52,10). The expected column is the product of the probability and the number of balls. The sum of the expected column shows us that on average the highest ball will be 48.18. Rounding to the nearest card, the highest expected card is the king of spades.
Highest of 10 Cards
| Highest Card | Probability | Expected |
|---|---|---|
| 10 | 0.000000000063 | 0.000000000632 |
| 11 | 0.000000000632 | 0.000000006953 |
| 12 | 0.000000003477 | 0.000000041719 |
| 13 | 0.000000013906 | 0.000000180784 |
| 14 | 0.000000045196 | 0.000000632742 |
| 15 | 0.000000126548 | 0.000001898227 |
| 16 | 0.000000316371 | 0.000005061939 |
| 17 | 0.000000723134 | 0.000012293281 |
| 18 | 0.00000153666 | 0.000027659882 |
| 19 | 0.00000307332 | 0.000058393084 |
| 20 | 0.000005839308 | 0.000116786168 |
| 21 | 0.000010616924 | 0.000222955411 |
| 22 | 0.000018579618 | 0.000408751587 |
| 23 | 0.00003144243 | 0.000723175884 |
| 24 | 0.00005165542 | 0.001239730087 |
| 25 | 0.000082648672 | 0.002066216811 |
| 26 | 0.000129138551 | 0.003357602319 |
| 27 | 0.000197506019 | 0.005332662506 |
| 28 | 0.000296259028 | 0.008295252787 |
| 29 | 0.000436592252 | 0.012661175306 |
| 30 | 0.000633058765 | 0.01899176296 |
| 31 | 0.000904369665 | 0.028035459607 |
| 32 | 0.001274339073 | 0.040778850337 |
| 33 | 0.001772993493 | 0.058508785267 |
| 34 | 0.002437866053 | 0.082887445794 |
| 35 | 0.003315497832 | 0.116042424112 |
| 36 | 0.004463170158 | 0.160674125694 |
| 37 | 0.005950893544 | 0.220183061136 |
| 38 | 0.007863680755 | 0.298819868684 |
| 39 | 0.010304133403 | 0.401861202713 |
| 40 | 0.013395373424 | 0.535814936951 |
| 41 | 0.017284352805 | 0.708658464999 |
| 42 | 0.022145577031 | 0.930114235312 |
| 43 | 0.028185279858 | 1.211967033891 |
| 44 | 0.035646089232 | 1.568427926212 |
| 45 | 0.044812226463 | 2.016550190844 |
| 46 | 0.056015283079 | 2.576703021634 |
| 47 | 0.069640622206 | 3.273109243697 |
| 48 | 0.086134453782 | 4.134453781513 |
| 49 | 0.106011635423 | 5.194570135747 |
| 50 | 0.129864253394 | 6.493212669683 |
| 51 | 0.158371040724 | 8.076923076923 |
| 52 | 0.192307692308 | 10 |
| Total | 1 | 48.181818181818 |
Although you didn't ask, the median card is the ace of clubs. The probability of the highest card falling under the ace of clubs is 41.34%, exactly on the ace of clubs is 10.60%, and higher than the ace of clubs is 48.05%.
I would deeply appreciate it if you could answer my question for me. I have e-mailed several poker pro’s including the Canadian one (Blount). Not one has answered my question. Most of them never even wrote back, including Blount. My question is - Could you please tell me the formula for figuring out the odds and percentages of getting the first two cards in hold’em and the percentage of that particular hand beating the other hands-assuming you know what they are-like you see on TV. I already know the formula and the easy way of figuring out you making your hand after the flop. I’m aware of the poker calculator but I would like to know the formula for my own knowledge. You hear about the pro’s knowing all the odds. I’m beginning to think it’s a bunch of bunk because not one person has answered my question. Thank you very much for taking all the time to read this.
There is no easy formula. Personally my program cycles through all the remaining cards and records how the number of hands that win for each player and takes a percentage based on those totals. I imagine everyone else either does that or is random simulation based.
(Bluejay adds: As for your doubting that pros really know the poker odds because they didn’t write back to you -- didn’t it occur to you that another likely explanation is that they didn’t care to serve as a free helpdesk to the whole world? Britney Spears must be a fraud because she never wrote back to me, either.)
In Texas hold em if a player accidentally shows his cards before betting round is complete is that player’s hand dead?
No. It would still be a live hand.
I am new to Texas Hold’em and my first book on the subject was Play Poker Like the Pros by Phil Hellmuth. After comparing his ’Top Ten’ Hold’em hands with yours, I have noticed major differences. For example, he has 7-7 as the tenth best and you rank this hand far down the list. There are other major discrepancies. I trust your analyses of various casino games and I wonder how your lists could be so different. Thank you.
Poker is a hard game to advise on because the behavior of other players is unknown. My model assumes all players stay in until the end of the hand, for the sake of simplicity. While I respect Phil’s opinion Get the Edge at Low-Limit Texas Hold’em by Bill Burton lists hands in three groups, and 7-7 is the lowest of pairs to play only in middle or late position. He says 6-6 should only be played in late position. In other words he doesn’t seem to think highly of 7-7 either.
In "Ken Warren Teaches Texas Hold ’Em" he states that against Pocket Aces (where the suits are the same color) that no other hand will win more often than 6/5 suited of the opposite color. I accept the fact that this hand will win 22.89% of the time in the above situation. However, there are twelve ways to arrange pocket aces, and only 2 of them include the situation above. My question is then: What is the best starting hand against 2 random aces?
The best hand against two random aces are the other two aces. Aside from that using my 2-player hold ’em calculator we can see the expected value (probability of winning less probability of losing) is greatest with a suited 5 and 6, whether or not one of the aces share the same suit as the 5 and 6. So against a random set of pocket aces the suited 5,6 is still better. To correct you, if you have a suited 5 and 6 and you know somebody else has pocket aces there is a 50% chance that one of them match your cards in suit.
Would you consider doing an analysis on Texas Hold’em Bonus? This game is all over Atlantic City and is also in the Las Vegas Flamingo. Thank you.
It just so happens that I have four computers cranking away on that game right now. The number of combinations in that game is so huge the game requires about 56 days of computer time to cycle through them all. I should have the analysis completed about October 20.
Party poker has added a side bet in Hold 'em. It pays 7 to 1 if the flop is all red or all black. (You must choose the correct color.) Is this a sucker bet, or should I be asking how bad of a sucker bet is this? Thanks for the great site.
Thanks for the compliment. The probability of that the flop will all be the same of a particular color is combin(26,3)/combin(52,3) = 2600/22100 = 2/17 = 11.765%. The expected return on this bet is (2/17)*7 - (15/17) = -1/17 = -5.882%.
I’m confused about your claim in the September 25, 2005 column that a suited 5/6 is the best hand to have against pocket aces in Holdem. While your program is undoubtedly right and squares with all the other programs, I am still a little puzzled as to why 5/6 is better than 6/7 (in the sense of losing less as opposed to winning more), especially when there are several obvious hands in which it is worse, namely the fact that the A234 set of straights all lose to four aces when that’s the fifth card, whereas the corresponding 2345 straight doesn’t have tis problem. There are some other anomalies I’m looking at, but what is interesting to me is that what seems like a pure logic problem is far from straightforward and requires a machine assist to guide intuition.
Okay, a suited 5/6 against pocket aces, both of different suits, will win 22.87% of the time, tie 0.37%, and lose 76.75%. A suited 6/7 will win 22.88%, tie 0.32%, and lose 76.80%. So the suited 6/7 will win 0.01% more. However the suited 5/6 is better because it ties 0.05% more. The reason for this seems to come down to the straights. There are going to be more waits to form a straight on the board if all the mid-cards in left in the deck. Removing a 7, as opposed to a 5, makes it more difficult to make straights with the remaining cards, thus making ties less likely, and thus the expected value less.
In Hold Em poker, does not burning cards affect the odds? Does burning cards affect the odds and game at all?
No. The probabilities do not change in any card gave by burning cards.
Party Poker has a high hand jackpot awarded to tables showing down a Royal Flush. What are the odds in a 10 handed Texas Holdem game of a table hitting a Royal Flush?
If we assume all hands are played to the end the probability of any given player having a royal flush is 4*combin(47,2)/combin(52,7) = 1 in 30,940. To make things simple lets assume each hand is independent. The probability of at least one player in 10 having a royal flush would be 1-(1-(1/30940))10 = 0.00032, or 1 in 3094.
We seem to have a debate in our office about showing your cards in Texas Hold’em. Can a player show his hole cards to the table if he decides to fold, even though there are players still betting? Is there an actual rule?
This is in very poor poker etiquette. If you did that in Vegas you would probably be warned not to do it again the first time. A second time and you would probably be made to leave the table.
In your article on Texas Hold’em Bonus I noticed that you’ve mentioned the only part of the strategy I have quantified is that the player should fold unsuited 2/3 to 2/7 under either set of rules, and unsuited 3/4 under the Atlantic City rules only. Are these the criteria you’ve created for your simulation? I would also be interested in how you determine whether to bet on the turn or river. I am trying to figure out what exactly would be "optimum" play. I also would like to know what exactly you mean by "expected" value of the initial hands. I guess in short, my question is how did you determine the optimal strategy for this game?
I realize it must be frustrating when I declare the house edge of game under optimal strategy but don’t state what the optimal strategy is, as is the case in Texas Hold’em Bonus. The reason for that is I don’t know what the optimal strategy is either. The number of combinations in most poker-based games is so vast that it would a very tedious and time consuming task to quantify exactly what the proper strategy is. Instead I program my computer to cycle through every possible set of cards and make the play with the highest expected value. The expected value is how much the player can expect to win (positive) or lose (negative). That greatly reduces the number of lines of code required. So there is no random simulation. My program looks into the future my looping through all possible combinations of cards and going with the play that results in the greatest win or least loss.
Is it required to flip over your cards if you call a player going all in? I’ve seen this done on television numerous times, but can I just wait until then end of the hand?
According to various sources it is required to turn your cards over in a tournament game, but optional in a cash game.
In your March 20 column, you answer a question about turning your Hold’em hand over once all-in and action is complete. You mentioned your friend was sort of unsure, so I can tell you that in virtually every major card room in America, the rule is this: In a NL tournament, you MUST turn your hand over as soon as all betting action is complete (i.e., all remaining players are all in. This speeds up play as it allows the winning hand to be determined much more quickly. In a NL cash game, it is OPTIONAL to turn over your all-in hand... in fact doing so is the mark of a novice and some consider it rude to turn it over before the river. So there you have it. - Pete from NY
I would like to respond to the question last week about turning over the cards in an all-in situation. I believe I read that one of the main reasons they require the cards to be shown in a situation such as the one above is more specific to tournament play. Requiring to show the cards helps identify possible collusion and the act of dumping chips from one player to another to assist a certain player in getting a chip advantage.
Thanks to both of you for the correction.
I made an all-in bet after the flop, the only guy left in the hand at the time thinks for a few seconds, shows me his hand. The cards never touched the table, he didn’t say a word, but I took this as him folding. I proceeded to muck my cards, and grab the chips, and he states that he hasn’t folded yet. Now he has seen my two cards, decides to call, and wins on the river card. Is this legal or not?
Poker is one of my weaker games when it comes to gambling so I turn again to J.B. for this one. Here is what he said.
That move is completely illegal. Anytime someone shows his cards to an opponent, the hand is dead. The only exception is when both players have declared themselves "all-in." At that point both hands are shown and the hand is completed. In this case, the guy that showed the cards to his opponent would forfeit the hand and the other guy would win.After I got this reply I recalled a scene in a movie, I think Stuey, in which one player offers to turn over one of his cards, chosen by the other player, for $100. I asked J.B. if the scene was realistic. Here is his response to that question.
This always used to happen in tournaments and was perfectly okay back then. It was around 2001 or 2002 that this rule was formally changed in almost all card rooms. I was in a tournament last week and was low on chips. I moved all-in with AQ suited. Everyone folded to the big blind who had lots of chips. After about two minutes of him thinking, he showed me the KQ he had and then went back to thinking about whether to call. I called the supervisor over and said he showed me his cards before making a decision and the hand should be dead. He agreed with me, the hand was automatically declared dead, and he was given a five-minute penalty where he had to leave the table, so it cost him about five hands. The blinds and antes were high, so the penalty cost him several thousand tournament chips.
In your recent Ask the Wizard column there was a question about a player showing cards before delcaring a decision in Hold’Em. Depending on house rules, this can be allowed in a heads up situation, where no other player is involved. (IE: It’s a hand in a ring game that is down to 2 players, OR it is a heads-up tournament) In a standard tournament you cannot expose your cards early (even if you are heads up with another player) becuase you are theoretically affecting everyone else still alive in the tournament.
You are the third person to claim that J.B.’s answer was incorrect. To get a disinterested third opinion I asked the poker foreman at the Red Rock hotel/casino. He said that exposing cards is not allowed in a tournament or if more than two players are still in the hand. However with only two players left in a cash game hand if one of them wants to be a fool and expose his cards that would be allowed at the Red Rock. I later asked the same question at the Wynn and the answer was the same.
An increasingly common side-bet I’m seeing in Texas Hold ’Em games is for players to bet on the total "value" of the flop, where the value of a card is assigned via Blackjack rules. (ie, A=11, KQJ10=10, others are face) Players have the option to pick one or more total value numbers by putting a side bet in the pot. Play continues until the flop hits a value that is covered by a player (so, a flop of KK4 would send the pot to a player that bet on 24). Mathematically, what is the best number to bet on? Most games I have played in have the stipulation that 30 cannot be bet on, which would make you think it would be the "best" number to bet on, but considering 30 has a very limited number of ways it can be made (three 10-value cards, A-9-10, or A-A-8) I’m not sure that that’s true. Also, hands where more players have ten-value and Ace cards are more likely to see a flop. Would you be interested in doing an analysis on this side-bet?
I’m going to assume that if nobody wins on the flop that either the bets are refunded or the next flop is used to resolve them, as opposed to the turn and river cards being used. I am going to ignore the rule that if everybody folds then the bet is not resolved. Clearly this rule helps the lower totals but to factor that in the analysis would get complicated and subjective. That said, the table below shows the probability of each total. As you can see, the best bet would be on a total of 23, with a probability of 8.3982%.
Blackjack Points in Flop
| Total | Combinations | Probability |
| 33 | 4 | 0.000181 |
| 32 | 96 | 0.004344 |
| 31 | 504 | 0.022805 |
| 30 | 840 | 0.038009 |
| 29 | 784 | 0.035475 |
| 28 | 920 | 0.041629 |
| 27 | 1108 | 0.050136 |
| 26 | 1264 | 0.057195 |
| 25 | 1472 | 0.066606 |
| 24 | 1652 | 0.074751 |
| 23 | 1856 | 0.083982 |
| 22 | 1800 | 0.081448 |
| 21 | 1508 | 0.068235 |
| 20 | 1408 | 0.06371 |
| 19 | 1336 | 0.060452 |
| 18 | 1196 | 0.054118 |
| 17 | 1080 | 0.048869 |
| 16 | 896 | 0.040543 |
| 15 | 740 | 0.033484 |
| 14 | 512 | 0.023167 |
| 13 | 352 | 0.015928 |
| 12 | 268 | 0.012127 |
| 11 | 200 | 0.00905 |
| 10 | 136 | 0.006154 |
| 9 | 92 | 0.004163 |
| 8 | 48 | 0.002172 |
| 7 | 24 | 0.001086 |
| 6 | 4 | 0.000181 |
Your site is awesome, I’ve learned so much from it. On the flop in holdem poker and you have 20 cards that give you the winning hand. Why is the percentage of you making your hand by the river 67.5% and not 86% (20/47 + 20/46)? I’ve looked everywhere and can’t seem to figure this out, even though I know it’s probably very elementary. I’d appreciate the help, Thanks!!
Thanks! Your way is double counting getting two of the 20 cards you need. The probability you get one of your 20 needed cards on the turn is 20/47 = 0.4255. The probability you don’t get it on the turn and then do get it on the river is (27/47)*(20/46) = 0.2498. So the total probability is 0.4255 + 0.2498 = 0.6753.
I don't know a lot about poker, but I do find it fun, so maybe you can clear something up for me. On a recent trip to Vegas with my wife, we stayed at Arizona Charlie's Decatur. Our reason for staying here was because they had advertised $2-$4 Hold 'em on their website. On our first morning, we walk down to the poker room and put our names in for $2-$4. I notice the poker guy writing our names under the columns for $4-$8. So I told him we wanted $2-$4 (there was a column labeled “$2-$4” on the same sheet). He said it was $2-$4: $2 before the flop, $4 after the flop, and $8 after the turn and river. I described to him what I meant by $2-$4: $2 before and after the flop and $4 after the turn and river. He laughed at us like we didn’t know what we were talking about and said that’s not how the game is played. We ended up playing poker at the Gold Coast the remainder of our trip. Is this type of betting normal for poker rooms? (I ended up telling the poker room supervisor if we could afford $4-$8 Hold ‘em, we wouldn’t be staying at Arizona Charlie’s.)
I agree that a "2/4" game means the bets are in $2 units before the turn and $4 after the turn. However, the small blind is likely be $1. It sounds like when Arizona Charlie's is calling a game "2/4" they are referring to the blinds, which would mean a small blind of $2, and a big blind of $4, which would imply $8 bets after the turn. I've never heard this usage before so I don’t blame you for being surprised.
p.s. I later received the following from Anthony, a poker room supervisor.
I am a poker room supervisor. I was just writing to let you know about the correct wording for the poker limits in Texas Hold 'em. If as game is referred to as $2/4. It is referring to the bets. (A game is only referred to by the blinds if it is No-Limit.) $2 pre flop and post flop,$4 on the turn and the river.A game that is listed as $2/$4/$8 (which is exactly what I suspect the previous letter writer was actually referring to, is $2 pre-flop,$4 post-flop,$8 turn and river .It is also possible to have a game listed as $2/$4/$6/$8. Just passing the information on, good poker supervisors want people to have as much information as possible.
Consider the 6,5 suited starting hand in hold em. According to your published odds, in a 2-player game, this hand is rated 128th out of 169 possible hands. But in a 10-player game, this hand is rated 61st out of 169 possible hands. I am very curious as to why this is the case. Thanks for your help.
Much of the value of suited connectors comes from the relatively high probability of forming a straight, flush, or straight flush. These are premium hands, which usually win against any number of players. In a two-player game you only are rewarded with one person’s money, but in a 10-player game you can milk it for a much larger pot.
I have a question that has caused a lot of discussion in our group. It concerns players that do not have enough chips to post the small blind (or big) blinds. Example: In tournament play, with blinds of 20/40. The player in the small blind position only has 15 chip value. Should that player be eliminated because he is unable to meet the blind value; or should he be allowed to play (all-in) the chips he has?
A player may call for less in that situation, but he may only win the amount of his call bet from each of the other players who posted the small blind. In the example above, 15 chips from each player posting the small blind would be put in the pot. All other money would be put in a side pot, which the short-stacked player would not be eligible to win.
My thanks to Ashley Adams for her help with this question.
In Colorado, each wager is capped at $5. In Texas Hold’em Bonus, the min/max ante is $5 and the min/max for the flop, turn and river is also $5. What is the impact of the flop bet equaling the ante as opposed to being twice the ante?
Assuming the player followed the strategy for the conventional Las Vegas rules, where the player wins the ante on a straight or higher, the house edge would go up from 2.04% to 3.51%. This I’m sure could be lowered with rule specific strategy changes. However, it takes my computer 71 days to analyze this game so please forgive me if I end my answer here.
I had a question that happened in my home tournament game the other night. The middle stack went all in and the short stack called. The short stack flipped over pocket aces, as we were chipping up the all in. The middle stack said you have me beat and tried to muck his hand. He slid them over to the dealer to be folded. Is a player allowed to fold his hand at that point if he chooses to muck? Another player in the hand said he could not fold so we ran out the hand. He caught a runner to hit a flush, however I considered the hand to be over since he verbally said I am beat and slid his cards to the dealer face down. I believe if his cards touched the muck pile they are dead, but is he allowed to fold at that point by choice. The middle stack was not that experienced and figured he was beat. I would greatly appreciate it if you could clear this up for us.
For the fine points of poker rules, I turned to my friend Jason for this one. Here is what he said, "This is very interesting. Anytime two cards hit the muck, the hand is dead without exception. However, since this was an all-in situation, this should not have happened. Any time someone is all-in in a tournament, all hands must be turned face up. If two of the players aren’t all-in, then play continues without all hands being exposed. My ruling would be the hand is dead, since he did muck his cards. Why he would do that is beyond me! Hope this helps a little."
I was recently in Las Vegas and played a new game for me -- World Poker Tour: All in Poker. I did not bet on the bonuses and used your advice on how to play the game. I bet $15 on the blind, so on average my overall bets were approximately $100. At one casino I was rated as a $15 player and at another a $45 player. I don’t understand why two casinos, both in the same corporate family, would give me two different ratings for the same bets in the same game, and I don’t understand why I wasn’t rated as a 90-100 player.
The first casino was correctly basing your bet size on the ante only. The second was counting the raise bets. If the second casino does include raises in the average bet then it should be using a lower house edge for purposes of rating. In my opinion many casinos do not comp players accurately. Each casino has its own policies, regardless of which corporate family it is in. What is important in your case is which casino gives you back the most for your play. There are lots of factors that go into that decision besides the average bet size.
Great site! A must see for Vegas newbies and those thinking of striking it rich through gambling. Is there an optimal ratio to wager between the ante and the bonus bet in the Texas Hold’em Bonus table game? Is it simply 10% bonus to ante since you calculated 90.4% of bonus bets are losers?
Thanks for the kind words. I get asked this question a lot regarding every game where there are two or more bets to choose from. You should bet 100% on the better bet. In the case of Texas Hold ’em bonus the element of risk on the ante is 0.53% and on the bonus bet it is 8.54%, assuming Vegas rules both ways. For comparing one bet to another I believe the element of risk should be used. So in this case, the ratio of ante bet to bonus bet should be infinity, because the bonus bet should be zero. Same thing with Three Card Poker, which is usually the venue this question is asked about. In that game you should bet 100% on the ante and 0% on the Pairplus.
I have a very complicated question, which divided a friend and me. In a three-person Texas Hold’em game two players hold K/3 off-suit, and one player has K/2 off-suit. Before the flop, which is the stronger hand the K/2 or either K/3?
The K/2 is much better, because the K/3 players may have to split the pot. As my three to five player Texas Hold’em calculator shows, the K/2 player can expect to win 42.96% of the pot, and each K/3 player 28.52%.
I just started playing no limit Texas Hold’Em. My question is, when the small and large blinds have been posted and everyone has either checked or called and then comes the flop, what is the minimum bet that has to be made? Does it have to be at least equal to the large blind, or can it be of any amount (including less then the large blind)? Is it different after the turn and river cards?
In a no limit game the minimum bet is whatever the big blind is. This is true at before and after the flop.
Hi almighty Wizard. My friends and I had a bet about Texas Hold’Em. They said 7/2 always is the worst hand you can have, no matter what your opponent has. But I said 6/2 would have less chance of winning facing 7/2 pre-flop. Who is right?
If a 7/2 off-suit faced off against a 6/2 off-suit, the possible outcomes would be as follows, according to my Texas Hold ’Em Calculator.
7/2 wins: 57.07%
6/2 wins: 25.13%
Tie: 17.80%
However that doesn’t prove that 7/2 is the superior hand in general. Considering only your own hand, according to my various power rating tables, 7/2 off-suit is worse than 6/2 off-suit. For four or fewer players, the worst hand is 3/2 off-suit.
So, if the bet was phrased as who would win between 6/2 and 7/2 offsuit, then you win. However that doesn’t prove that 7/2 is the better hand in general, only for that one situation.
Hi -- great site! Hope you can stand one more Texas Hold ’Em Bonus question, since there’s a different variation where I play, in Colorado. Unlike the Vegas and Atlantic city rules, in Colorado all bets must equal $5 (the table minimum equals the $5 bet limit imposed by CO law), so the flop bet must equal (not double) the ante bet. Otherwise, the game rules appear to match the Vegas version you analyzed.
Thanks. Normally the house edge in Texas Hold ’Em Bonus is 2.04% under the Vegas rules and 5.59% under the Atlantic City rules. You are indeed right that no single wager can be over $5 in Colorado. Under the Colorado version of the rules, you describe above, the house edge is 2.35%.
I’ve heard in poker games the term "strangle the blind" or similar to that. What is that?
I asked my friend Jason about this one. Here is what he said:
"I think what she means is a blind straddle. What that means is the person who acts after the big blind makes a raise of two times the big blind, before looking at his or her hand. This is usually done to stimulate action at a table where the pots have been small with lots of pre-flop folding. Let’s say it’s a $6-$12 limit hold ‘em game, with the small blind $3 and the big blind $6. I am in the position next to the big blind and I straddle the pot by making it $12 before I look at my cards." — Jason
Playing in a poker league one night and this came up. Blinds were $300/$600 and the first to act bet $2,000 and then the next two folded when it was my turn. Not seeing the original bet, I bet $3,000 without saying raise or call since I thought I was the first to bet. I started to pull back $1,000 and call but was told that my chips had to stay in and that I would have to put in another $1,000 to raise the first bet or just flat out muck my hand. Could you please give me the proper ruling on this situation. Thank you.
I think neither of you is right. It is correct that when you put in more than $2,000, you were implying you were raising the pot. The minimum raise should have been $1,400, for a total bet of $3,400, contrary to the table ruling. This is because the last bet of $2,000 was a $600 call and $1,400 raise. Your bet was only a $1,000 raise. So, you needed to put in another $400, or muck your hand. (source)
Do you believe players who win something in a live poker tournament should give an additional tip if they bought a "dealer’s add-on" at the beginning of the tournament? I play in a lot of small buy-in tournaments that use these add-ons, and the winners are always reminded that "tips are greatly appreciated." It seems to me that I have already tipped, even in the tournaments I don’t cash, and additional tipping just reduces whatever small edge I may have in a form of gambling that is already hard to beat (due to "vig," formats that diminish importance of skill, etc.) On the other hand, I don’t want to seem stingy. What do you suggest?
I don’t play much poker, so had to ask David Matthews what a "dealer’s add-on" is. Here is what he said.
The dealer’s add on is an additional and optional fee you’re given when you register. The add-on money is given to the dealers only as a way of compensating them for their time dealing the tourney. Normally you get an additional number of starting chips, 2500 instead of 2000, for example.I agree with Dave. Let me take that further by saying I also oppose shaking down players in tournaments with optional fees like re-buys and wild card purchases, unless those fees are somehow returned to the players, which is not the case usually. If the tournament would otherwise not be profitable for the casino, please just drop the pretenses and make the players pay more up front to enter.Tipping whether you buy the add-on or not should always be optional. If I had bought the add-on I would be less inclined to tip. By the way, I always buy the add-on. I am not sure if it’s mathematically correct from an EV standpoint but it just seems like the thing to do if I’m going to play the tourney in the first place.
If there were no dealer add-on, I do think it is appropriate for the winners to tip the dealers. If forced to say, I would suggest 1% to 2% of the win, and the less the win, the greater the percentage. In the situation in question, I would reduce the tip by the product of the total dealer add-on money and the ratio of my win to the total win. If that makes the tip zero or negative, then you do have a dilemma. I would probably do as I do when restaurants put on a mandatory 18%-20% tip, just put down a token small amount for appearances’ sake.
Why does your hand ranking chart differ from the one by David Sklansky (published in his book Hold ’Em Poker for Advanced Players, which also appears in the Wikipedia entry for Texas hold ’em starting hands? For example, Sklansky ranks 76 suited and A9 offsuit equally with a 5 rating. Your chart ranks 76 suited as an "11" but ranks A9 suited as a "16"! Care to explain why there are these discrepancies?
I think you misread Skanskey’s table. He rates 7-6 suited equally with A-9 off-suited with a 5. I rate 7-6 suited with an 11, and A-9 off-suited as a 10. So we both put them about the same.
At the Buffalo Thunder casino in Santa Fe, NM, there is a progressive side bet in Ultimate Texas Hold ’Em that I have never seen before. Do you have any odds on it?
Thanks for the information. I address that in my page on Ultimate Texas Hold ’Em.
Do you believe players who cash in a live poker tournament should give an additional tip if they bought a "dealer’s" add-on at the beginning of the tournament? I play in a lot of small buy-in tournaments that use these add-ons, and the winners are always reminded that "tips are greatly appreciated." It seems to me that I have already tipped, even in the tournaments I don’t cash, and additional tipping just reduces whatever small edge I may have in a form of gambling that is already hard to beat (due to "vig," formats that diminish importance of skill, etc.) On the other hand, I don’t want to seem stingy. What do you suggest?
For the benefit of other readers, a "dealer’s add on" is an optional purchase of additional chips in a poker tournament. Usually the cost per chip is less for the dealer’s add on than the original entry fee, in which case buying it is a good value. To answer your question, I think you are perfectly justified in reducing the tip if you come in the money, whether or not you purchased the dealer’s add on. I would liken it to tipping at a restaurant if they already added an 18% service fee. An appropriate winner’s tip, in my opinion, is whatever the dealers would have been tipped had they been dealing cash games over the duration of the tournament, less whatever they took in from the dealer’s add on.
Let me use this opportunity to state that I oppose all additional tournament costs, unless the extra money paid goes into the prize pool, which is usually not the case. Tournaments are usually structured in a way that paying the additional fees are a good value, so most players invoke the right, including me. Your odds of winning are significantly reduced if you don’t. However, if every player pays the additional fees, then they should drop the pretenses and just charge more for the tournament in the first place.
I don’t understand how it is that in your Texas Hold ’Em power tables A-7 ranks lower than KJ suited but on your calculator A7 has higher probabilty of winning.
Good question. For the benefit of other readers, here are the odds against a random hand with each of those two starting hands in a two-player game:
K-J Suited vs. A-7 Off-Suit
| Hand | Win | Lose | Draw | Expected Value |
K J J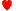 |
0.6148 | 0.3634 | 0.0218 | 0.2513 |
A 7 7 |
0.5717 | 0.3949 | 0.0334 | 0.1768 |
However, according to my Two-Player Texas Hold ’em Calculator, the probabilities of these two hands facing each other are:
A7 wins = 53.52%
KJ wins = 46.10%
Tie = 0.39%
So KJ suited is ranked higher in my table, but inferior to the A7 unsuited head to head. Why?
The answer is hard to explain. With two hands going against each other, you have to consider how they interact with each other. For example, in the table of starting hand strength, AK off-suit is only slightly better than AQ off-suit, with expected values of .3064 and .2886 respectively. However, if you pit them against each other, the AK crushes the AQ, as follows:
AK wins = 71.72%
AQ wins = 23.69%
Tie = 4.58%
In the A7-offsuit vs. KJ-suited, the ace towers over the king and jack. The greatest chance of the KJ player winning is if he pairs up the K or J and no aces appear. I show the probability of that is 37.73% only. The rest of the 46.10% probability of the KJ winning comes from higher hands.
While A7 is strong against KJ, it is more often dominated than KJ by random hands.
Maybe this is a bad comparison, but it is kind of like the game rock paper scissors. Among skilled players, individually each throw should have about the same power rating. However, if one player throws paper and the other scissors, the power ratings mean nothing, and scissors will win.
I’d be interested in your thoughts about a poker dispute I observed at the Wynn. Here is the executive summary. One player called "all in" and pushed his stack of chips towards the pot. Another player called, and lost. The dealer started to count the chips, which included two $100 black chips hidden amongst a lot of $1 blue chips and $5 red chips. It turns out the first player had them at the bottom of his blue and red stacks. The second player argued he wouldn’t have called if he had known about the black chips. The Wynn ruled in favor of the first player, but the first player was furious about it. Did the Wynn make the right ruling?
I’m not an expert on the fine points of poker rules, so I turned to David Matthews on this one. Here is what he says:
I play a lot of poker, mostly 2-5 NL and 5-10 NL. The rule is that oversized chips should be visible in front or on top, and if the dealer had known there were black chips, then the dealer should have requested that they be displayed. There is the conundrum of if the chips are hidden, how is the dealer going to see it? Stacks are also supposed to be one denomination. A stack of red ($5) chips on top of a $1 chip is considered a dirty stack because if someone were to eyeball the stack, they would likely guess the wrong number for the value. In this case, it would only be a $4 difference, but that’s the way it is. Interestingly, a stack of red chips with a $1 chip on top is not a dirty stack. I really think the dirty stack rules are a bit too much hassle.Whether the chips were visible or not is a real problem in no-limit hold ’em, because as is demonstrated in this situation, there can be confusion. Unfortunately, the ruling by the Wynn poker staff was the correct one, but it really was unfortunate for the person with the losing hand.
I have had a similar situation cost me $600. I went all in on a bluff against a guy, and he had a bunch of chips on top of some bills. $100 bills play in most places in town. I said to him, "What do you have? 2 Bills?" He just nodded and didn’t say anything. I went all in. He called instantly with 3 kings. He actually had 8 bills, and the house made me pay it. I would not have tried the bluff for an "All in" had I known how much money he had. That was expensive.
That’s why I ALWAYS ask on all ins. Even if a guy has 5 red chips ($25) and he throws it in, I ask the dealer how much it is. Dealers get irritated sometimes and look at me like, "It’s pretty obvious, isn’t it?" Also, players give me a hard time, too, sometimes. They tell me it’s obviously $100 or whatever it looks like. Doesn’t matter. I ask, "How much is it?" over and over again.
Another thing is I will usually bet a number rather than say "all in." If I had made a bet of $500 against the guy with the 3 kings, then it wouldn’t have mattered how many bills or what kinds of chips he had. I would have been on the hook for the $500 only.
I’m personally against having bills play on the table, because I constantly have to ask people how many bills. People get offended when you ask them over and over again, especially when they have less money on the table than other players, because they’re embarrassed to say, "2 bills." And then every hand I’m in with them I ask again, because you never know if maybe they added some bills to their stack in between hands. Or maybe they won a hand you didn’t see. In addition, just the fact that you ask someone how much they have might give away information about your hand.
I think paper should not play, and on 2-5 games and lower, the largest chips allowed in play should be $100 chips. My opinion isn’t a popular one, though.
This question was raised and discussed in the forum of my companion site Wizard of Vegas.
What is supposed to happen in a poker game if a player dies mid-hand?
I asked a former Nevada gaming regulator and casino president about this. He said it would be treated as an "all in" kind of situation, much the same way an accidental disconnection is handled in Internet poker.
In other words, a side pot would be made of chips in the middle at the time of death. Then, any additional bets would be set aside in a separate pot. If the dead player had the highest hand, then he would win the side pot. Win or lose, any chips he had on the table after the hand would be set aside for the deceased's estate.
This question was raised and discussed on my forum at Wizard of Vegas.
Which starting hand has the highest chance of winning against a pair of random aces in a two-player game of Texas Hold 'Em?
Using my Texas Hold 'Em calculator, I show the answer is suited 5-6. If the 5-6 is in a different suit from both aces, the probability of winning is 22.87% and a tie 00.37%. If the 5-6 is in the same suit as one of the aces, then the probability of winning is 21.71% and a tie 00.46%. On average, the player with 5-6 suited will lose 0.55005 units, assuming he bet one unit, and have a chance of winning, given that there is a winner, of 22.383%.




