On this page
Wild! Wild! Wild!
Introduction
Wild! Wild! Wild! is a video poker variant attached to multi-play video poker. If the player bets 10 credits per play, the game will randomly add one to three wild cards to the deck with certain probabilities. The price to invite this feature is 5 credits per play.
Rules
- Wild! Wild! Wild! is an optional feature added to multi-play video poker.
- If the player bets one to five coins per play, the game will play like conventional multi-play video poker, which I assume the reader is familiar with.
- If the player bets ten coins per play, he will invoke the feature. Wins will be based on five coins bet per play, with the other five coins considered a fee a pay for the feature.
- Depending on the game and pay table, the game may add 1 to 3 wild cards to the deck. For example, in 9-6 Jacks or Better, the probabilities of added wilds are as follows:
- 0 added = 40%
- 1 added = 19%
- 2 added = 21%
- 3 added = 20%
- The game does inform the player the player how many wilds were added.
- If the player invokes the feature, in addition to the wild cards, the game will boost the pay table wins and add wins for a five of a kind in what are normally not wild card games.
Example

In the image above two wilds were added to the deck. You can tell because it says so right above the credit meter of 9280. On the deal I got one of them.

In the image above, I choose to hold the wild card and the suited ace and king.
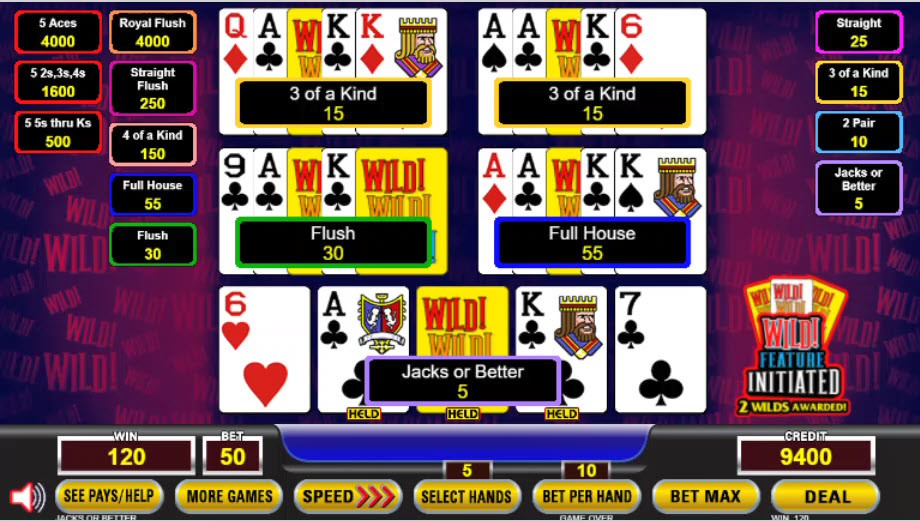
After the draw, two hands improve to a three of a kind, one to a flush, one to a full house and one remains a high pair. The total "win" is 5 + 2*15 + 30 + 55 = 120 credits. The bet amount was 5*10 = 50 credit, so the actual profit was 70 credits.
Analysis
The following is my analysis of 9-6 Jacks or Better. First I will present four return tables, for 0 to 3 wild cards added. In each table, the return column is the produce of the win, probability and 0.5. The reason for dividing by 2 is wins are based on half the bet amount.
9-6 Jacks or Better — Zero Wilds Added
| Event | Pays | Probability | Return |
|---|---|---|---|
| Royal Flush | 800 | 0.000025 | 0.009911 |
| Five Aces | 800 | 0.000000 | 0.000000 |
| Five 2's, 3's, 4's | 320 | 0.000000 | 0.000000 |
| Five 5's Through K's | 100 | 0.000000 | 0.000000 |
| Straight Flush | 50 | 0.000109 | 0.002714 |
| Four of a Kind | 30 | 0.002353 | 0.035294 |
| Full House | 11 | 0.011452 | 0.062984 |
| Flush | 6 | 0.010865 | 0.032596 |
| Straight | 5 | 0.014599 | 0.036499 |
| Three of a Kind | 3 | 0.073596 | 0.110394 |
| Two Pair | 2 | 0.127355 | 0.127355 |
| Jacks or Better | 1 | 0.207471 | 0.103735 |
| Trash | 0 | 0.552176 | 0.000000 |
| Total | 1.000000 | 0.521481 |
9-6 Jacks or Better — One Wild Added
| Event | Pays | Probability | Return |
|---|---|---|---|
| Royal Flush | 800 | 0.000146 | 0.058600 |
| Five Aces | 800 | 0.000008 | 0.003078 |
| Five 2's, 3's, 4's | 320 | 0.000021 | 0.003362 |
| Five 5's Through K's | 100 | 0.000065 | 0.003265 |
| Straight Flush | 50 | 0.000486 | 0.012148 |
| Four of a Kind | 30 | 0.008626 | 0.129386 |
| Full House | 11 | 0.015754 | 0.086649 |
| Flush | 6 | 0.014272 | 0.042816 |
| Straight | 5 | 0.018712 | 0.046781 |
| Three of a Kind | 3 | 0.134392 | 0.201587 |
| Two Pair | 2 | 0.111222 | 0.111222 |
| Jacks or Better | 1 | 0.221151 | 0.110575 |
| Trash | 0 | 0.475144 | 0.000000 |
| Total | 1.000000 | 0.809470 |
9-6 Jacks or Better — Two Wilds Added
| Event | Pays | Probability | Return |
|---|---|---|---|
| Royal Flush | 800 | 0.000451 | 0.180569 |
| Five Aces | 800 | 0.000040 | 0.016104 |
| Five 2's, 3's, 4's | 320 | 0.000092 | 0.014786 |
| Five 5's Through K's | 100 | 0.000295 | 0.014734 |
| Straight Flush | 50 | 0.001025 | 0.025623 |
| Four of a Kind | 30 | 0.019494 | 0.292415 |
| Full House | 11 | 0.018932 | 0.104127 |
| Flush | 6 | 0.013721 | 0.041164 |
| Straight | 5 | 0.022243 | 0.055608 |
| Three of a Kind | 3 | 0.186878 | 0.280317 |
| Two Pair | 2 | 0.097005 | 0.097005 |
| Jacks or Better | 1 | 0.237120 | 0.118560 |
| Trash | 0 | 0.402702 | 0.000000 |
| Total | 1.000000 | 1.241014 |
9-6 Jacks or Better — Three Wilds Added
| Event | Pays | Probability | Return |
|---|---|---|---|
| Royal Flush | 800 | 0.001098 | 0.439188 |
| Five Aces | 800 | 0.000121 | 0.048501 |
| Five 2's, 3's, 4's | 320 | 0.000235 | 0.037537 |
| Five 5's Through K's | 100 | 0.000761 | 0.038037 |
| Straight Flush | 50 | 0.001621 | 0.040520 |
| Four of a Kind | 30 | 0.033008 | 0.495117 |
| Full House | 11 | 0.020270 | 0.111484 |
| Flush | 6 | 0.012974 | 0.038921 |
| Straight | 5 | 0.027422 | 0.068556 |
| Three of a Kind | 3 | 0.226116 | 0.339174 |
| Two Pair | 2 | 0.084512 | 0.084512 |
| Jacks or Better | 1 | 0.249475 | 0.124738 |
| Trash | 0 | 0.342387 | 0.000000 |
| Total | 1.000000 | 1.866286 |
The following table summarizes the return by the number of wilds added. The lower right cell shows a return of 99.63%.
9-6 Jacks or Better — Return Summary
| Wilds | Probability | Average Win | Expected Win |
|---|---|---|---|
| 0 | 0.400000 | 0.521481 | 0.208593 |
| 1 | 0.190000 | 0.809470 | 0.153799 |
| 2 | 0.210000 | 1.241014 | 0.260613 |
| 3 | 0.200000 | 1.866286 | 0.373257 |
| Total | 1.000000 | 0.000000 | 0.996262 |
The following table also summarizes the whole game according to each paying hand. The lower right cell again shows a return of 99.63%.
9-6 Jacks or Better — Overall Return Table
| Event | Pays | Probability | Return |
|---|---|---|---|
| Royal Flush | 800 | 0.000352 | 0.140855 |
| Five Aces | 800 | 0.000034 | 0.013667 |
| Five 2's, 3's, 4's | 320 | 0.000070 | 0.011251 |
| Five 5's Through K's | 100 | 0.000226 | 0.011322 |
| Straight Flush | 50 | 0.000675 | 0.016879 |
| Four of a Kind | 30 | 0.013275 | 0.199131 |
| Full House | 11 | 0.015604 | 0.085820 |
| Flush | 6 | 0.012534 | 0.037602 |
| Straight | 5 | 0.019551 | 0.048877 |
| Three of a Kind | 3 | 0.139441 | 0.209161 |
| Two Pair | 2 | 0.109347 | 0.109347 |
| Jacks or Better | 1 | 0.224697 | 0.112349 |
| Trash | 0 | 0.464193 | 0.000000 |
| Total | 1.000000 | 0.996262 |
The following set of tables show the pay tables available for each game, the probabilities for 1 to 3 wilds, the 5-coin return and 10-coin return. You can see the 10-coin return is always a little higher.
Triple Triple Bonus
| Pay Table | One Wild | Two Wilds | Three Wilds | 5 Coin Return | 10 Coin Return |
|---|---|---|---|---|---|
| 9-6 | 33.8% | 16.2% | 1.0% | 0.997516 | 0.998125 |
| 9-5 | 34.2% | 15.8% | 1.0% | 0.986087 | 0.988065 |
| 8-5 | 34.5% | 15.5% | 1.0% | 0.975516 | 0.978888 |
| 7-5 | 35.0% | 15.0% | 1.0% | 0.964948 | 0.967663 |
| 6-5 | 35.5% | 14.5% | 1.0% | 0.954392 | 0.956614 |
Double Double Bonus
| Pay Table | One Wild | Two Wilds | Three Wilds | 5 Coin Return | 10 Coin Return |
|---|---|---|---|---|---|
| 9-6 | 22.0% | 24.0% | 5.0% | 0.989808 | 0.992654 |
| 9-5 | 23.0% | 23.0% | 5.0% | 0.978729 | 0.979416 |
| 8-5 | 23.0% | 23.0% | 5.0% | 0.967861 | 0.973390 |
| 7-5 | 24.0% | 22.0% | 5.0% | 0.957120 | 0.960078 |
| 6-5 | 24.0% | 22.0% | 5.0% | 0.946569 | 0.954316 |
Triple Double Bonus
| Pay Table | One Wild | Two Wilds | Three Wilds | 5 Coin Return | 10 Coin Return |
|---|---|---|---|---|---|
| 9-7 | 32.9% | 14.1% | 4.0% | 0.995778 | 0.997753 |
| 9-6 | 33.8% | 13.2% | 4.0% | 0.981540 | 0.982452 |
| 9-5 | 34.0% | 13.0% | 4.0% | 0.970204 | 0.974809 |
| 8-5 | 34.7% | 12.3% | 4.0% | 0.959687 | 0.962143 |
| 7-5 | 35.0% | 12.0% | 4.0% | 0.949178 | 0.953411 |
The 8-5 pay table for Bonus Poker is the only one where the wild card probabilities are not exact as shown. The are based on the following weights:
- 0 wilds = 355
- 1 wild = 100
- 2 wilds = 440
- 3 wilds = 100
Bonus Poker
| Pay Table | One Wild | Two Wilds | Three Wilds | 5 Coin Return | 10 Coin Return |
|---|---|---|---|---|---|
| 8-5 | 10.0503% | 44.2211% | 10.0503% | 0.991660 | 0.993538 |
| 7-5 | 11.5% | 43.0% | 10.0% | 0.980147 | 0.980517 |
| 6-5 | 10.0% | 43.0% | 10.0% | 0.968687 | 0.968874 |
Double Bonus Poker
| Pay Table | One Wild | Two Wilds | Three Wilds | 5 Coin Return | 10 Coin Return |
|---|---|---|---|---|---|
| 9-7-5 | 15.0% | 31.0% | 5.0% | 0.991065 | 0.991211 |
| 9-6-5 | 15.5% | 30.5% | 5.0% | 0.978062 | 0.981317 |
| 10-6-4 | 16.0% | 30.0% | 5.0% | 0.974613 | 0.975721 |
| 9-6-4 | 16.5% | 29.5% | 5.0% | 0.963754 | 0.966398 |
| 9-5-4 | 17.5% | 28.5% | 5.0% | 0.952738 | 0.953866 |
Jacks or Better
| Pay Table | One Wild | Two Wilds | Three Wilds | 5 Coin Return | 10 Coin Return |
|---|---|---|---|---|---|
| 9-6 | 19.0% | 21.0% | 20.0% | 0.995439 | 0.996262 |
| 9-5 | 19.5% | 20.5% | 20.0% | 0.984498 | 0.986314 |
| 8-5 | 20.5% | 19.5% | 20.0% | 0.972984 | 0.974251 |
| 7-5 | 19.5% | 20.5% | 20.0% | 0.961472 | 0.963206 |
| 6-5 | 20.0% | 20.0% | 20.0% | 0.949961 | 0.953392 |
Bonus Poker Deluxe
| Pay Table | One Wild | Two Wilds | Three Wilds | 5 Coin Return | 10 Coin Return |
|---|---|---|---|---|---|
| 9-6 | 20.8% | 25.2% | 5.0% | 0.996417 | 0.997437 |
| 9-5 | 21.5% | 24.5% | 5.0% | 0.985495 | 0.986541 |
| 8-5 | 22.0% | 24.0% | 5.0% | 0.974009 | 0.977041 |
| 7-5 | 24.0% | 22.0% | 5.0% | 0.962526 | 0.962659 |
| 6-5 | 24.5% | 21.5% | 5.0% | 0.953611 | 0.958094 |
Deuces Wild
| Pay Table | One Wild | Two Wilds | Three Wilds | 5 Coin Return | 10 Coin Return |
|---|---|---|---|---|---|
| 20/12/9/5/3 | 18.0% | 22.0% | 20.0% | 0.989378 | 0.992907 |
| 25/15/10/4/3 | 15.5% | 24.5% | 20.0% | 0.989131 | 0.990747 |
| 25/15/10/4/3 | 16.0% | 24.0% | 20.0% | 0.975791 | 0.975823 |
| 25/16/13/4/3 | 16.8% | 23.2% | 20.0% | 0.967651 | 0.968383 |
| 25/15/10/4/3 | 18.0% | 22.0% | 20.0% | 0.948182 | 0.952554 |
Deuces Wild Bonus
| Pay Table | One Wild | Two Wilds | Three Wilds | 5 Coin Return | 10 Coin Return |
|---|---|---|---|---|---|
| 9/4/4/3 | 19.0% | 21.0% | 20.0% | 0.994502 | 0.998339 |
| 13/4/3/3 | 21.0% | 19.0% | 20.0% | 0.988025 | 0.989615 |
| 10/4/3/3 | 21.0% | 19.0% | 20.0% | 0.973644 | 0.978256 |
| 12/4/3/2 | 21.5% | 18.5% | 20.0% | 0.962183 | 0.966031 |
| 10/4/3/2 | 21.5% | 18.5% | 20.0% | 0.953368 | 0.959245 |
Acknowledgements
I would like to thank VideoPoker.com for the math on this page as well as permission to use the screenshots in the example section.
External Links
Discussion about this game in my forum at Wizard of Vegas.




